バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
形式ニューロンについての解説。
形式ニューロンの概念図とか数式とか。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】形式ニューロンへ至る道

まずは、形式ニューロンへ至る道を再掲。
- ヘヴィサイド関数(済)
- 形式ニューロン
- 分類問題のHelloWorld
- 誤差関数
- 決定境界直線
- 決定境界直線の特定方法
- 総当たり法による分類

今回は形式ニューロンの説明がメイン。
形式ニューロンの概念図

前回は、ヘヴィサイド関数の話から入ったけど、
肝心の形式ニューロンの話がまだだね。

それを今回説明しよう。
まずは概念図。
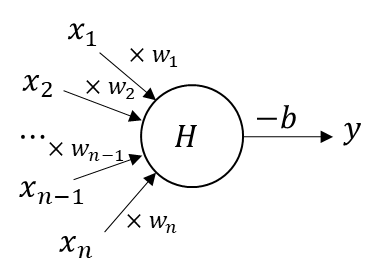

\(x\)が入力ベクトル、
\(y\)が出力、
\(w\)が重み、
\(b\)がバイアス
\(H\)がヘヴィサイド関数
になる。

なんか、こういう絵ってニューラルネットワークでよく見る気がする。

そうだね。
まぁ違いとしては、
バイアスが負になってる点と
活性化関数がヘヴィサイド関数ってところだな。

確かに細かいところは違うのか。
形式ニューロンの数式表現

形式ニューロンの数式表現も載せておこう。
\(
y=H\Bigg(
\begin{bmatrix}
w_1&w_2&\dots&w_{n-1}&w_n&-b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_{n-1}\\
x_n
\end{bmatrix}
\Bigg)
\)

重み\(w\)と入力\(x\)は内積をやってるだけなのか。

その結果をヘヴィサイド関数に渡して、0 or 1を出力するって仕組みだね。

確かによく聞くニューロンの振る舞いっぽい!

まぁ、この構成はいろいろ問題があるから、現在に於いてはほぼ使われてはいないのだけど、
パーセプトロン、ニューラルネットワークの基本構成の元にはなってるという位置づけになる。

基礎の基礎って感じでちょっと面白くなってきた気がする。
まとめ

まとめだよ。
- 形式ニューロンの概念図を説明。
- よく見るニューロンの概念図と類似。
- 形式ニューロンの数式を説明。
- 重みと入力の内積の結果をヘヴィサイド関数に渡して0or1にしている。
バックナンバーはこちら。




コメント