バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の拡張と言われている射影変換の話。
射影変換の理屈について
- 基本ベクトルと基底ベクトル
- 元画像平面を3次元空間で表現
について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
【再掲】射影変換の理屈の因果関係

まずは大まかな流れを再掲
- 大まかな理屈(済)
- 大まかな理屈を座標変換で説明(済)
- 基本ベクトルと基底ベクトル
- 元画像平面を3次元空間で表現
- 3次元空間を地面平面に落とし込む
- 一連の座標変換まとめ
- 方程式の変形
- 行列表現
- アフィン変換との関係性
- 係数の求め方
- 係数の求め方(行列表現)
- 射影変換の処理の流れ

「大まかな理屈を座標変換で説明」というところまで終わっている。
基本ベクトルと基底ベクトル

直接的に射影変換には関連しないのだが、
基本ベクトルと基底ベクトルについて簡単に説明しておこう。

ベクトルにようわからん種類があるんか・・・。

これはそれほど複雑な話ではない。
まずはこの図を見てみよう。
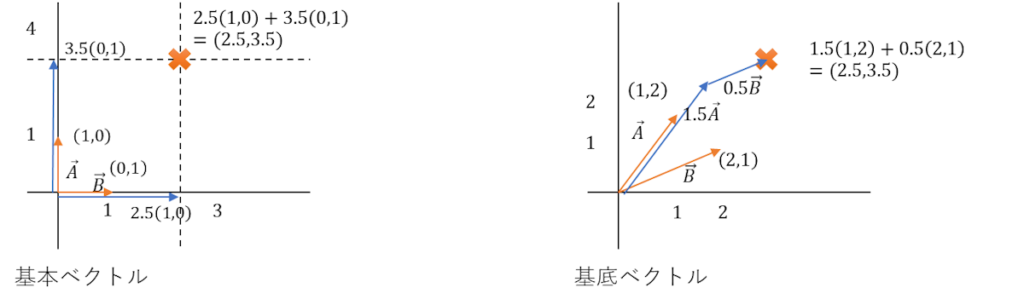

基本ベクトルの方は、平面上のベクトル表現の基本系って感じはする。

基本ベクトルの認識はそれで正しい。
軸に沿った2本の単位ベクトル(大きさ1)になる。
これがあれば、すべての平面座標を表現できる。

基底ベクトルがわからんな・・・。

基底ベクトルは
2本の交差するベクトル。
このベクトルも、すべての閉演座標を表現できる。
図の例では、(1,2)、(2,1)の2つのベクトルがあるが、
これを任意の倍率且つ合成すれば、あらゆる座標が表現可能だ。
基本ベクトルは、強烈な制約のついた基底ベクトルと言える。

なるほど。
確かに表現できるかと言えば表現できるね。
元画像平面を3次元空間で表現

そして、話を射影変換に戻し・・・。

元画像を3次元空間で表現しなおすのだけど、
この画像のように解釈する。
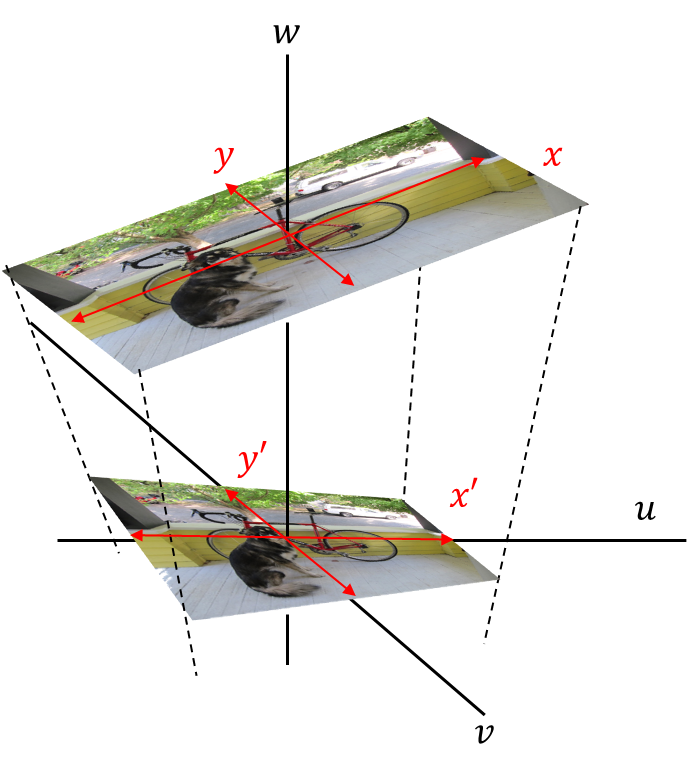

\((x,y)\)と\((u,v,w)\)は線形変換で求められる。
少なくとも2次関数とかにはならない。
よって、以下の変換式が成立するはず。
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
u=ax+by+c \\
v=dx+ey+f\\
w=gx+hy+i
\end{array}
\right.
\end{eqnarray}
\)

まぁ、感覚的には正しい気がする。

数学的に表現するならば、
「\(x,y\)を基底ベクトルとし、加えて、\(w\)方向の基本ベクトル。
この3つのベクトルの合成は全空間を表現できる。」
ってことになるな。

あー、ここで基本ベクトル、基底ベクトルの話が出てくるのか。
まとめ

まとめだよ。
- 基本ベクトルと基底ベクトルについて説明。
- 元画像平面を3次元空間で表現した場合の式を説明。
- ここで基本ベクトル、基底ベクトルの話が出てくる。
バックナンバーはこちら。




コメント