バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の拡張と言われている射影変換の話。
射影変換の理屈について
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
射影変換の理屈

今回は射影変換の理屈について説明してくれるんだっけ?

そうなのだが、
割とボリュームがあるから、
まずは全体像としてどうなのかを見せよう。
- 大まかな理屈
- 大まかな理屈を座標変換で説明
- 基本ベクトルと基底ベクトル
- 元画像平面を3次元空間で表現
- 3次元空間を地面平面に落とし込む
- 一連の座標変換まとめ
- 方程式の変形
- 行列表現
- アフィン変換との関係性
- 係数の求め方
- 係数の求め方(行列表現)
- 射影変換の処理の流れ

なんかやべぇ感じしかしねぇ・・・。

一個一個はそれほど難しくはない。

そうなんだろうけど、
数が多いのと因果関係が難しいから一個一個が簡単でもトータルだと簡単じゃなくなるんだよなぁ・・・。

因果関係はシンプルで、上から順番に因果があると思えばOKだな。
大まかな理屈

まずは大まかな理屈。
これは画像で説明した方が早い。
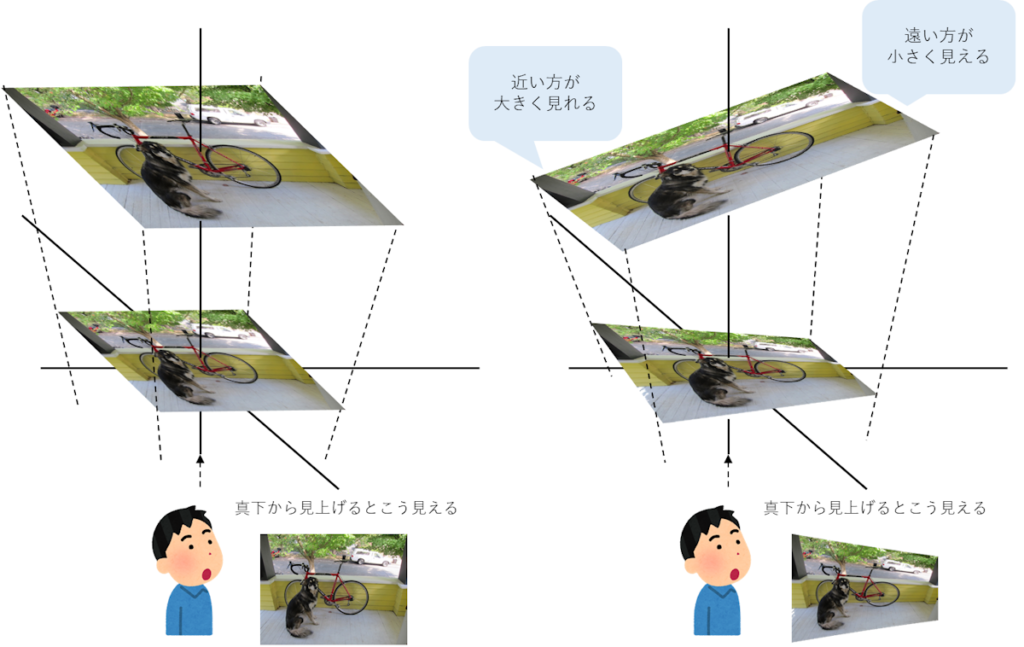

考え方としては思ったよりもシンプルかな。
3次元空間で見た場合、近い方が大きく見えて、遠くの方が小さく見えるのは感覚的にもわかる。

いや、でも、これが分かったからと言って、
計算方法は全く思いつかん。

まぁ、大まかな理屈に過ぎないからね。
これを一つ一つひも解いて、これから説明していく感じだな。
大まかな理屈を座標変換で説明

先ほどの大まかな理屈を座標変換で表現すると以下のイメージになる。
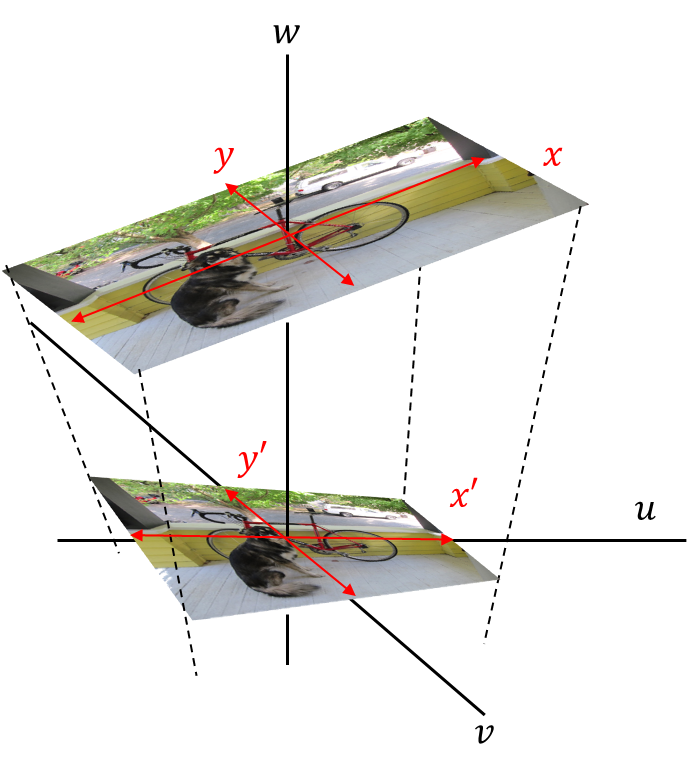

元画像の平面を\(x,y\)平面。
2種類の画像が存在数r空間を\(u,v,w\)空間。
射影が映り込む平明を\(x\prime,y\prime\)平面。
って感じだ。
よって、
\((x,y)\)→\((u,v,w)\)→\((x\prime,y\prime)\)
って流れで変換していく。

さっきよりかは具体的な表現にはなったが、
それでも意味わからん。

まぁ、一つずつひも解いていこう。
まとめ

まとめだよ。
- 射影変換の理屈を把握するための流れを記載。
- 大まかな理屈について説明。
- 大まかな理屈を座標変換で表現したパターンで説明。
バックナンバーはこちら。




コメント