バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換のアフィン行列は合成できる。
今回は、行列の結合法則について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
行列の結合法則の証明(行列サイズ一致の確認)

前回は\(\sum\)の性質についてだったね。

ここでは行列の結合法則の証明を行う。
ちなみに前回の\(\sum\)の性質を使うから復習しておくように。

(めんどくせぇな。)

以下の3つの行列があるとする。
A行列:\(l\times m\)行列
B行列:\(m\times n\)行列
C行列:\(n\times p\)行列

行列の積はできるけど、任意のサイズの行列ってことか。

まず、\((AB)C\)と\(A(BC)\)の行列のサイズが一致するか確認しておく。
\((AB)C\)の場合
\(
\begin{eqnarray}
&&\Big(l\times m) \times (m\times n) \Big)\times (n\times p)\\
&=&(l\times n)\times (n\times p)\\
&=&(l\times p)
\end{eqnarray}
\)
\(A(BC)\)の場合
\(
\begin{eqnarray}
&&(l\times m) \times \Big((m\times n) \times (n\times p)\Big)\\
&=&(l\times m) \times (m\times p)\\
&=&(l\times p)
\end{eqnarray}
\)

行列のサイズとしては一緒になるようだね。
行列の結合法則の証明(任意成分の証明)

次は任意の成分に着目した証明だ。
\(AB\)の任意成分(i,k)
\(
\displaystyle\sum_{j=1}^m a_{ij}b_{jk}
\)
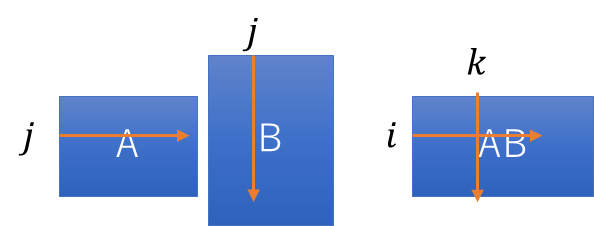
\((AB)C\)の任意成分(i,l)
\(
\begin{eqnarray}
&&\displaystyle\sum_{k=1}^n\bigg(\sum_{j=1}^m a_{ij}b_{jk}\bigg)c_{kl}\\
&=&\sum_{j=1}^m \sum_{k=1}^n a_{ij}b_{jk} c_{kl}
\end{eqnarray}
\)
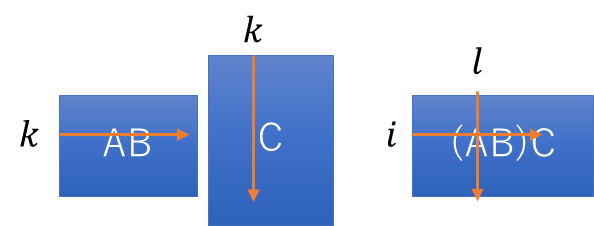
\(BC\)の任意成分(j,l)
\(
\displaystyle\sum_{j=1}^m b_{jk}c_{kl}
\)
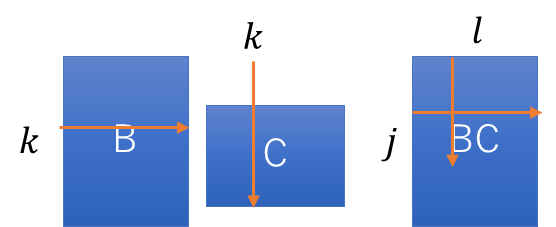
\(A(BC)\)の任意成分(i,l)
\(
\begin{eqnarray}
&&\displaystyle\sum_{j=1}^n a_{ij}\bigg(\sum_{k=1}^n b_{jk}c_{kl}\bigg)\\
&=&\sum_{j=1}^m \sum_{k=1}^n a_{ij}b_{jk} c_{kl}
\end{eqnarray}
\)
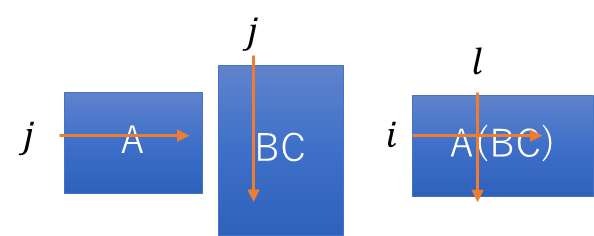

というわけで、行列の結合法則は成立する。

おー!
よくわからんが、キレイにまとまった感はある!

(「ようわからんが」って・・・ま、いっか)
まとめ

まとめだよ。
- 行列の結合法則を証明。
- サイズの証明と任意成分の証明に分かれる。
- ともに証明ができ、行列の結合法則は成立する。
バックナンバーはこちら。




コメント