バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の続き。
今回は、プログラミングに向けての話の続き。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
アフィン変換のプログラミングに向けて【再掲】

アフィン変換のプログラミングに向けての話の続きだねー。

全体の流れを再掲しておこう。
- 画像サイズの取得
- 中心を0とした座標系の生成
- X軸、Y軸ともに-1~1の範囲の座標系として扱う
- 座標\(x\prime,y\prime,1\)の3次元ベクトル配列の生成。
- ※ 全座標に対して一括でアフィン逆変換を実施するため。
- 変換元座標の算出(アフィン逆変換)
- 画像と同一形状の2次元配列に変換元座標配列を生成。
- 変換元の座標系-1~1をピクセル位置に変換。
- 元画像と変換元座標を元に変換先へコピー。

確か、「変換元座標の算出(アフィン逆変換)」までやった感じだ。
画像と同一形状の2次元配列に変換元座標配列を生成。

前回、アフィン逆変換を一括でできるよう、
入力、出力の列ベクトルを拡張した形として行列にした。
これを再度、座標系の構成に直すって感じだな。
イメージ的にはこんな感じ。
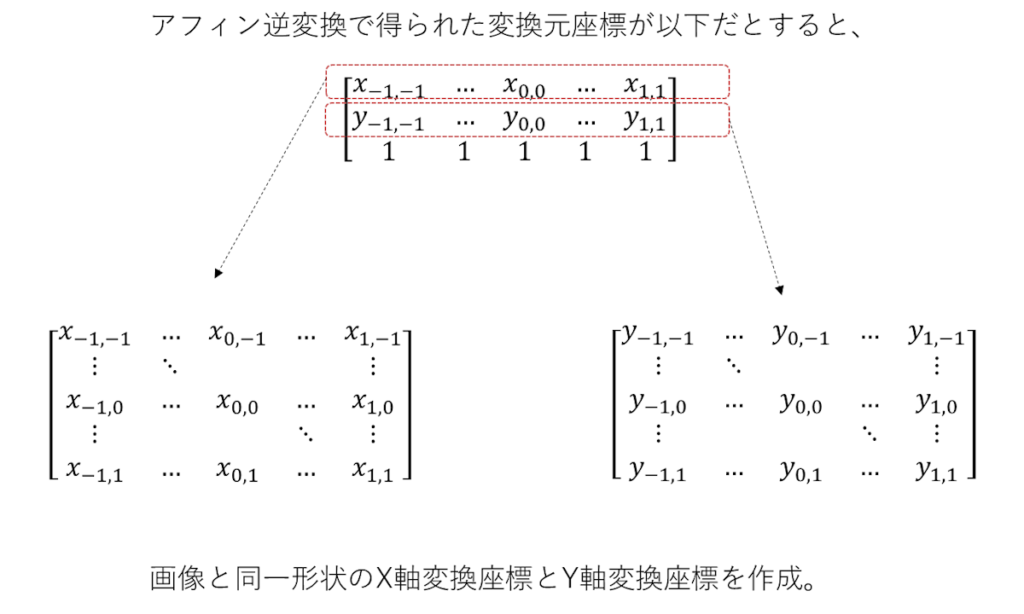

演算都合で1次元的にしたものを2次元平面に戻す作業だね。
これはやりたいことはわかる。
変換元の座標系-1~1をピクセル位置に変換。

次は、「変換元の座標系-1~1をピクセル位置に変換。」
これも変換都合で変形したものを再度元に戻す作業だな。

まぁ、演算都合にしたものを描画都合に直してるってことだね。

イメージ的には以下になる。

元画像と変換元座標を元に変換先へコピー。

そして、「元画像と変換元座標を元に変換先へコピー。」
変換座標の情報を元に実際のピクセルコピー作業だ。

そっか。
アフィン変換の段階では変換先と変換元の座標を求めただけだから、
まだ画像そのものは生成してないのか。

そうそう。
変換元から変換先にコピーだと、まだら模様問題が発生するので、
変換元から変換先を特定して、漏れなくコピーする方式だ。
処理イメージは以下になる。
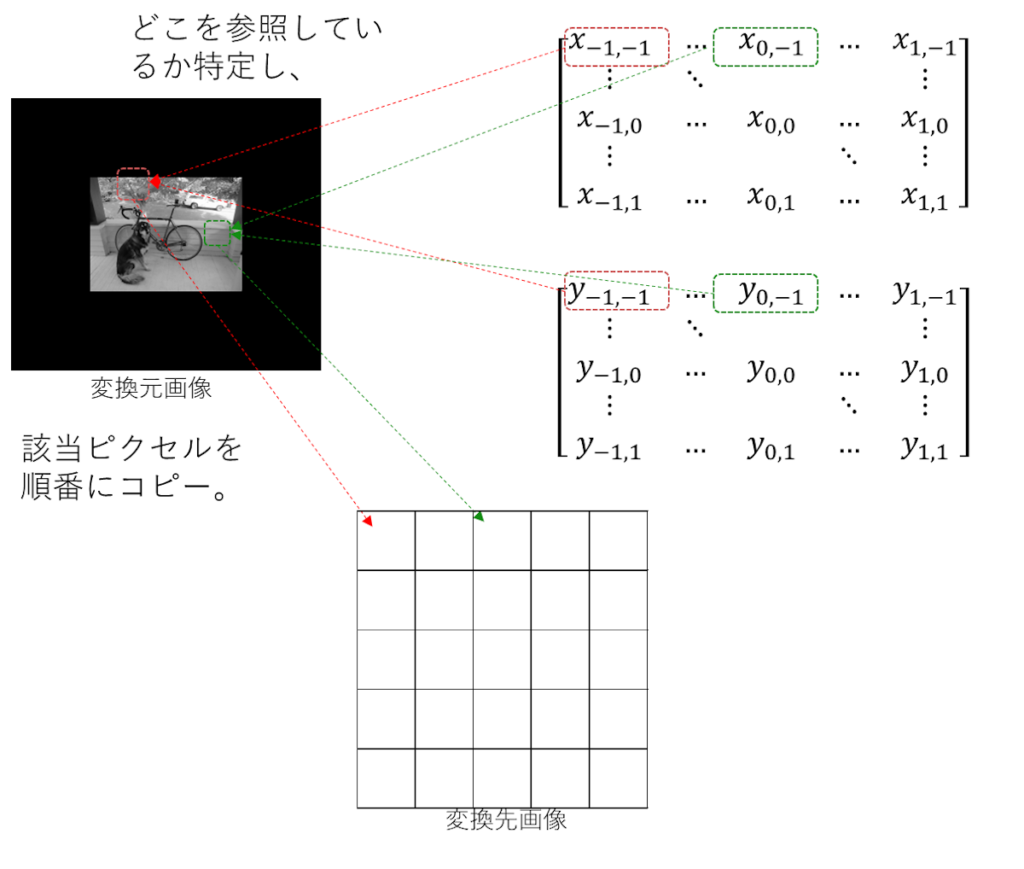

これができれば、各ピクセル情報が確定するから画像として扱える状態になる感じだね。

その後の画像保存は従来と一緒だから割愛だ。

というわけで、次回からは実際のプログラミングだね。
まとめ

まとめだよ。
- アフィン変換のプログラミングに向けてを再確認。
- 画像と同一形状の2次元配列に変換元座標配列を生成。
- 変換元の座標系-1~1をピクセル位置に変換。
- 元画像と変換元座標を元に変換先へコピー。
バックナンバーはこちら。




コメント