バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の続き。
今回は、プログラミングに向けての話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
アフィン変換のプログラミングに向けて

もう必要な情報はそろったでしょー。

うむ。
そろそろプログラミングし始めても良いレベルだろう。
しかし、事前に何をどのようにやるかの確認は必要だ。

まずは処理の流れの確認だねー。

以下の流れを想定している。
- 画像サイズの取得
- 中心を0とした座標系の生成
- X軸、Y軸ともに-1~1の範囲の座標系として扱う
- 座標\(x\prime,y\prime,1\)の3次元ベクトル配列の生成。
- ※ 全座標に対して一括でアフィン逆変換を実施するため。
- 変換元座標の算出(アフィン逆変換)
- 画像と同一形状の2次元配列に変換元座標配列を生成。
- 変換元の座標系-1~1をピクセル位置に変換。
- 元画像と変換元座標を元に変換先へコピー。

なんか、予想よりもやること多いぞ!!

まぁ、変換前の準備と後処理がいろいろ入ってるからねー。
画像サイズの取得と中心を0とした座標系の生成

画像サイズの取得はわかるけど、
中心を0とした座標系の生成ってのはなんだ?

画像の中心を原点とした回転をしたいからね。
原点が中心じゃないと困る。
画像で示すとこんな感じだな。
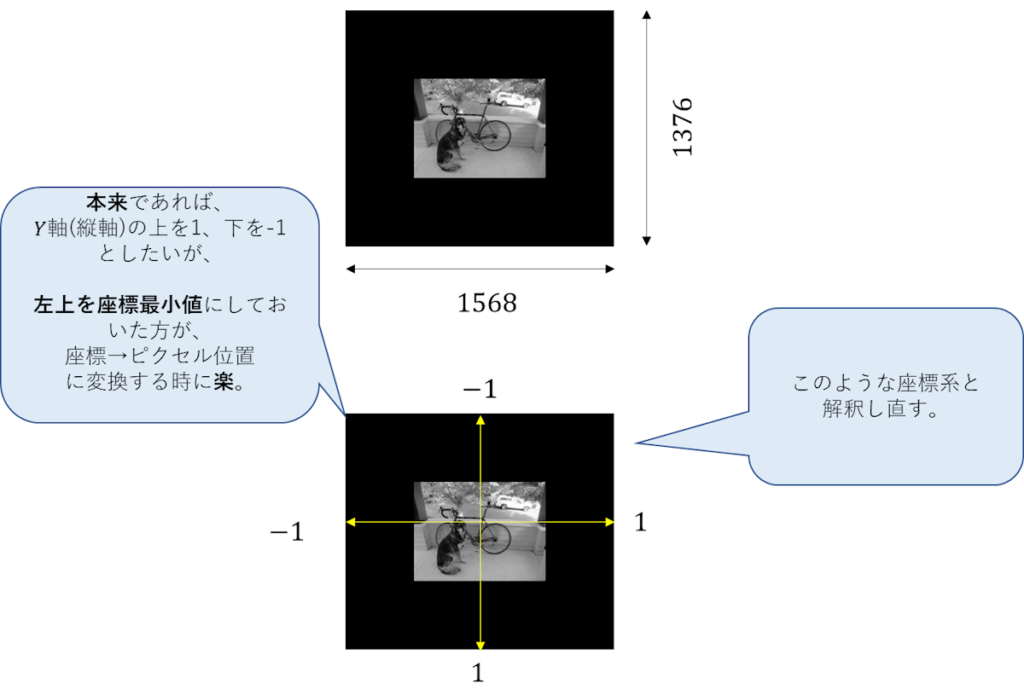

とりあえず、ピクセル座標からいい感じに座標を置き換えるってことだね。
座標の3次元ベクトル配列の生成。

その次の
「座標\(x\prime,y\prime,1\)の3次元ベクトル配列の生成。」
が何言ってるのかわからん。

まぁ、各ピクセルの座標を作った段階では2次元配列になるんだけど、
それを1次元配列的な形に変形するって話だな。
まず、座標配列である、2次元グリッドを作る。
だいたいどのツール、言語でもmashgridという関数があるから、これをしようすると簡単に作れる。
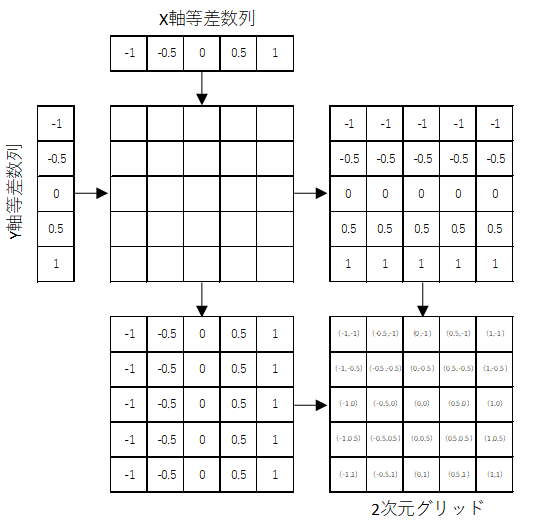

そして、このままだと2次元配列なので、1元配列な構成に変更。
reshapeや行列の数列展開を使用すると実現できる。
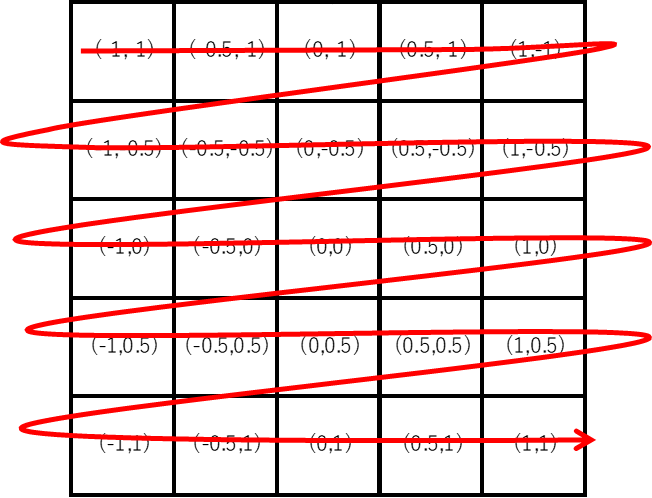

あー、やりたいことのイメージはわかったかな。

でも、なんでこんなことをするんだ?
変換元座標の算出(アフィン逆変換)

アフィン逆変換を一括でやるためだな。
まずアフィン逆変換の式を再掲する。
\(
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}=
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}\\
\)

これだと一つずつのピクセルの座標変換しかできない。
これを一括で出来るように式を拡張する。
\(
\begin{eqnarray}
\begin{bmatrix}
x_{(-1,-1)} & \dots & x_{(0,0)} & \dots & x_{(1,1)} \\
y_{(-1,-1)} & \dots & y_{(0,0)} & \dots & y_{(1,1)} \\
1 & 1 & 1 & 1 & 1
\end{bmatrix}=\\
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
-1 & -0.9 & \dots & 0 & \dots & 0.9 & 1\\
-1 & -1 & \dots & 0 & \dots & 1 & 1\\
1 & 1 & 1 & 1 & 1 & 1 & 1
\end{bmatrix}\\
\end{eqnarray}
\)

あー、なるほど。
入力ベクトル、出力ベクトルが列ベクトルなのを拡張して、
入力ベクトル群としての行列、出力ベクトル群としての行列にしているのか。

そうそう。
まぁfor文で回しても良いのだけどね。
数式の段階で解決してしまった方が楽だろう。
まとめ

まとめだよ。
- アフィン変換のプログラムの流れを確認。
- 中心を0とした座標系の生成。
- 3次元ベクトル配列の生成。
- アフィン変換を一括で行うため。
バックナンバーはこちら。




コメント