バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
アフィン変換の続き。
まだら模様問題の対策としてシンプルな手法について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
まだら模様対策のシンプルなやつ

前回は、アフィン変換のまだら模様問題の原因と対策の話だったけど、
対策としてはシンプルは手法があるんだよね?

そうそう。
画像で示すとこんな感じになる。
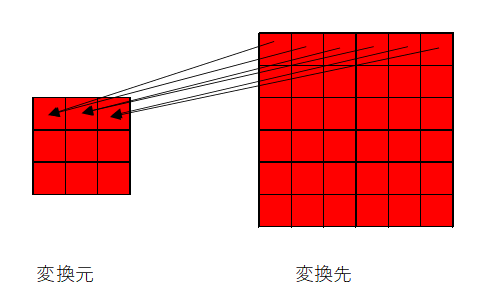

んー?
どういうことだ?
矢印の方向が、
変換元から変換先
じゃなくて、
変換先から変換元
になってる?

そうそう。
変換元から変換先にコピーするとピクセルが足りなくなるから、
だったら、変換先の全ピクセル位置から変換元を参照する方式にすれば、
ピクセルが足りないという事象は起きない。

なるほど!
確かにそれだったら全ピクセルが埋まるから、まだら模様が発生しない!
で、具体的にはどうするのか?

と思ったけど、具体的にはどうするんだ?
変換元から変換先にコピーするのがアフィン変換で、
それを逆向きにするのってできるの?

できる。
いわゆるアフィン逆変換。

(またやべぇ単語が出てきたぞ。)
アフィン逆変換

まず、アフィン変換の数式を再掲しよう。
\(
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}=
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\)

そうそう。
画像で示すとこんな感じになる。
\(
\begin{eqnarray}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}&=&
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}\\
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}&=&
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}\\
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}&=&
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}\\
\end{eqnarray}
\)

お!なんか割とさくっと求まったな。
そうか、逆行列を使えばいいのか!

そうそう。
代表的なアフィン変換

そして、そろそろ実際のプログラムを作成していきたいところだが・・・。

まだなんかあるんか・・・。

いや、代表的なアフィン変換のパラメータの設定方法の確認をするだけだ。
これをやっておかないと、アフィン行列にどういう値を設定して良いかがわからないからね。

たしかにアフィン変換の数式はわかったけど、何をどうしたらどうなるかはわからんな。

というわけで次回にそれらを確認する。
まとめ

まとめだよ。
- まだら模様対策のシンプルなやつを確認。
- アフィン逆変換を使う。
- アフィン逆変換は、アフィン変換の式を変形しただけ。
- アフィン行列が逆行列になる。
バックナンバーはこちら。




コメント