バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
非極大値抑制なるものの説明続き。
- 非極大値抑制の大雑把な雰囲気
- 2次元平面に実施する場合の考え方
- 勾配の特定方法
- 斜面の方向パターン
の「勾配の特定方法」について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
勾配の特定方法

前回で、いろんな方向から極大値を見つける必要があるってのはわかったけど、
どうしたら良いかがよくわからないんだよね。

実は、Sobelフィルタの時にこれを実現し得る情報をすでに得ている。

え?そうなの?

Sobelフィルタって横方向と縦方向のエッジ検出を合成したと思うけど、
その時に横方向ことx軸、縦方向ことy軸のを得ている。

確かに、途中経過として出してはいるね。

これらは、各方向の濃淡であり、これを利用すると濃淡の斜面の方向が分かるようになる。

ちょっと何言ってるのかわからない・・・。

x方向が1で、yが0なら横方向の斜面。
x方向が0で、yが1なら縦方向の斜面。
x方向が1で、yが1なら斜め方向の斜面。
まぁ、実際は切りの良い数値にはならなから、もっと細かい、360°のどこの方向を向いている斜面かが特定可能だ。

うーん、またイマイチ飲み込めてない感じはあるが、
言わんとすることは分かるかな。

そして、それを角度に表現しなおせば、どの方向の斜面に対して極大値を評価すれば良いかが確定する。

んー、角度に直せるの?

arctan関数を使えば一撃。
arctan関数

arctan関数!!
なんか脳がその情報を拒否する!!

そんな複雑なものじゃないよ・・・。
tan関数の逆関数だ。

tan関数って、直角三角形の縦÷横をした結果だよね・・・。

そうそう。
厳密には角度θが分かっていれば、縦÷横の結果を算出できるもの。
だな。

で、arctan関数は何してくれるの?

「縦÷横」が分かっていれば、角度θが求められる。
濃淡の勾配を求める雰囲気

まず、濃淡のx,yと濃淡斜面方向角度の関係を図示すると以下になる。
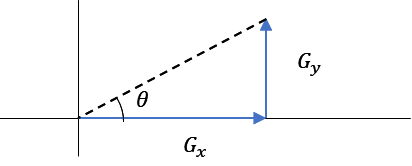

そして、これをtan関数を使って表現すると以下になる。
\(
\displaystyle\tan(\theta)=\frac{G_y}{G_x}
\)

まぁ、tan関数の定義そのものだよね。

これをtan関数の逆関数である、arctanで表現しなおす。
\(
\displaystyle\theta=\tan^{-1}\frac{G_y}{G_x}=\arctan\frac{G_y}{G_x}
\)

おー!?
arctan関数、むっちゃ便利関数じゃない?!

そうそう。
だから、この便利関数を利用すれば一撃で濃淡の勾配方向角度が求められる。
まとめ

まとめだよ。
- 非極大値抑制の「勾配の特定方法」について解説。
- 2次元平面で考えるためには勾配の方向が重要。
- 勾配の方向は、横、縦それぞれの傾斜度合いから推定可能。
- 実際にはarctan関数を使用する。
- arctan関数はtan関数の逆関数。
- 実際にはarctan関数を使用する。
バックナンバーはこちら。




コメント