バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
畳み込み演算の微分フィルタの話。
エッジ検出と言えば微分。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
エッジ検出するためには?

で、エッジを検出する方法だけど、
if文の嵐なプログラム以外にどう解決するの?

要は、山と谷がある部分が協調されれば良い。
山と谷は変化の激しい部分だ。

変化が激しいと値が大きくなる計算方法がある。
さて、これは何だろうか?

(質問してるのはこっちなのだが・・・。)

変化・・・変化・・・値が動く・・・。

あ!
微分か?!

正解!
簡単に微分っぽいことを実現するには?

いや、ちょっとまって、
微分するには、導関数を導出して・・・。
画像の導関数ってなんだ??

別に導関数の導出は不要だ。
値の差を求めるだけでOKだ。
そして、今回は、山と谷を知りたいだけなので、
完璧な微分をする必要はない。
微分と同じ効能を得られる演算をすればOKだ。

その微分と同じ効能ってのはどうすれば得られるの?

tanh関数で畳み込み積分をする。

畳み込み積分?
やりたいのは微分で積分じゃないんだけど・・・。

畳み込み積分ではあるが、tanh関数で畳み込むと微分相当の結果になる。

?????

tanh関数は、「ハイパボリックタンジェント」と言って、
こんな関数になる。
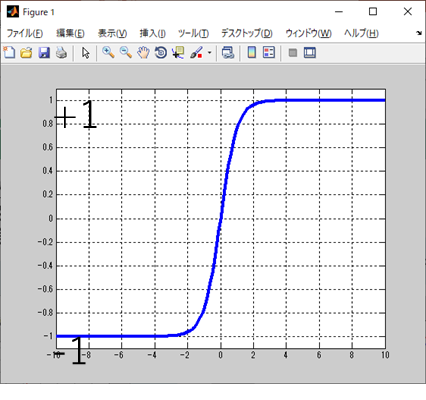

ニューラルネットワークの活性化関数とかで見たことあるような気がする。
tanh関数を使って畳み込み積分

このtanh関数を使って畳み込み積分をするとこうなる。
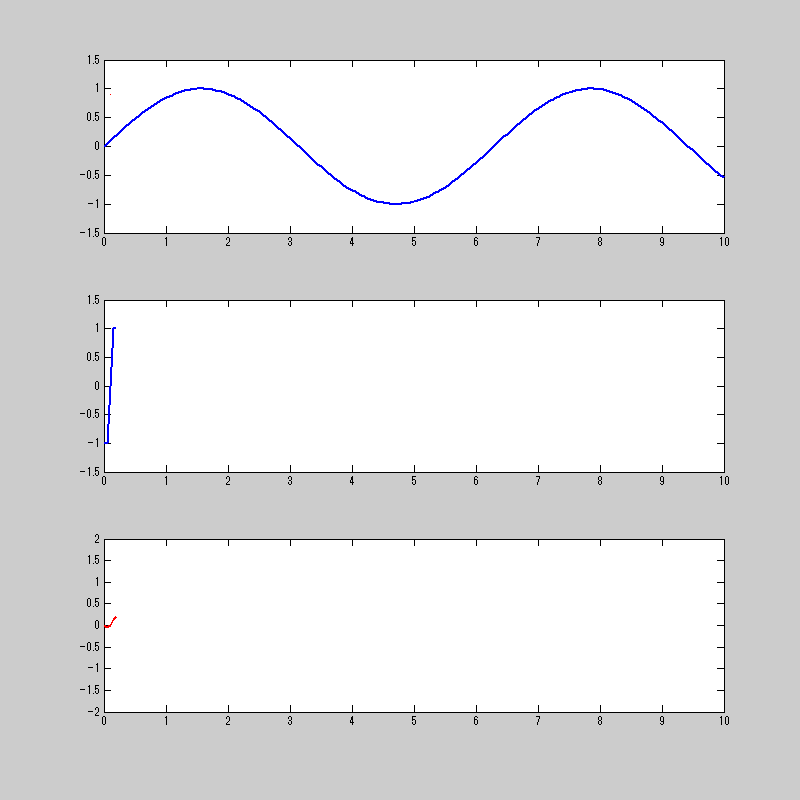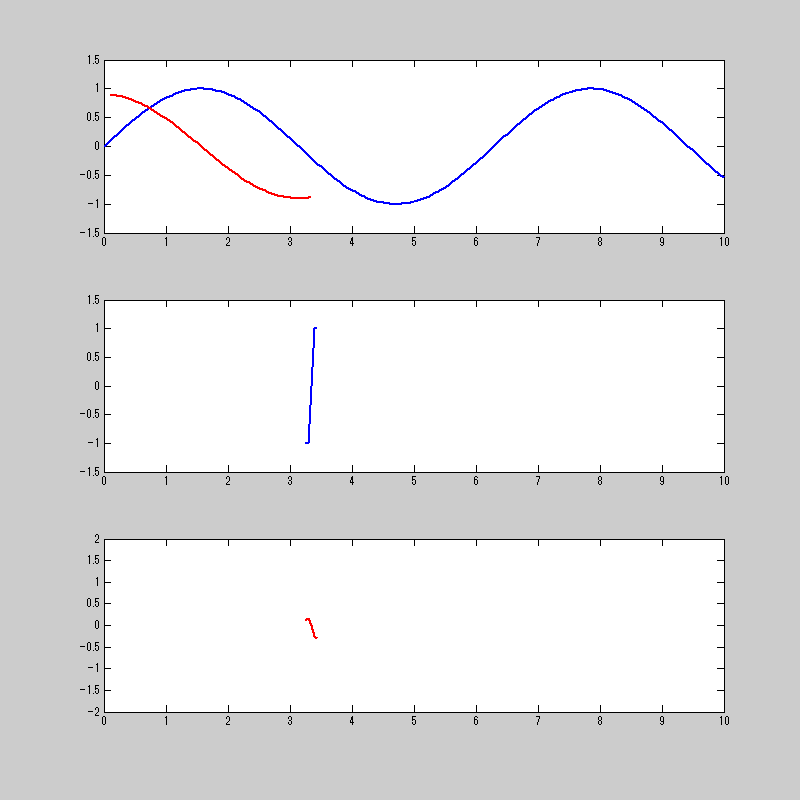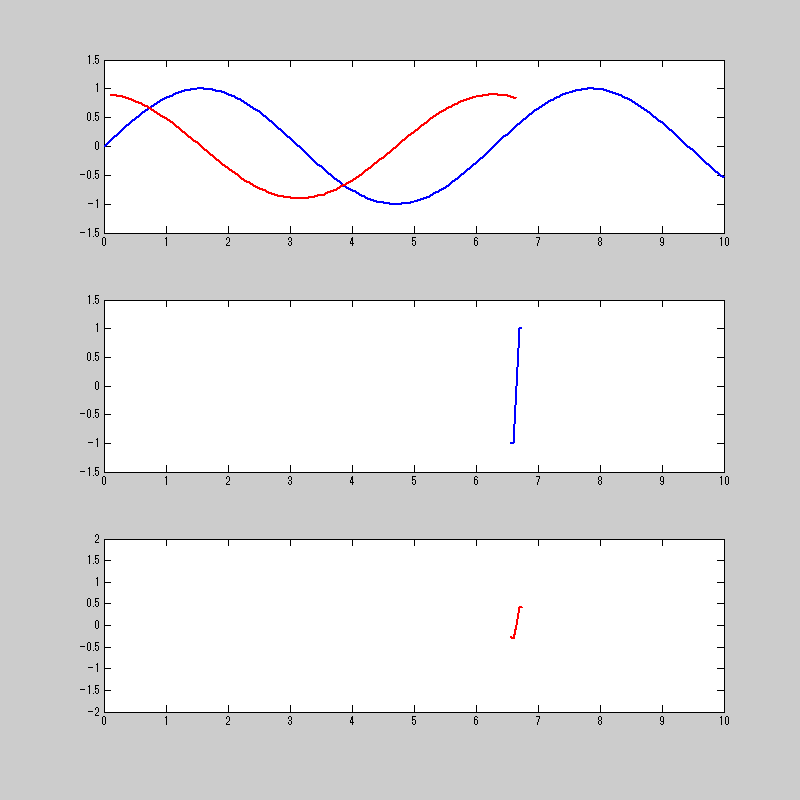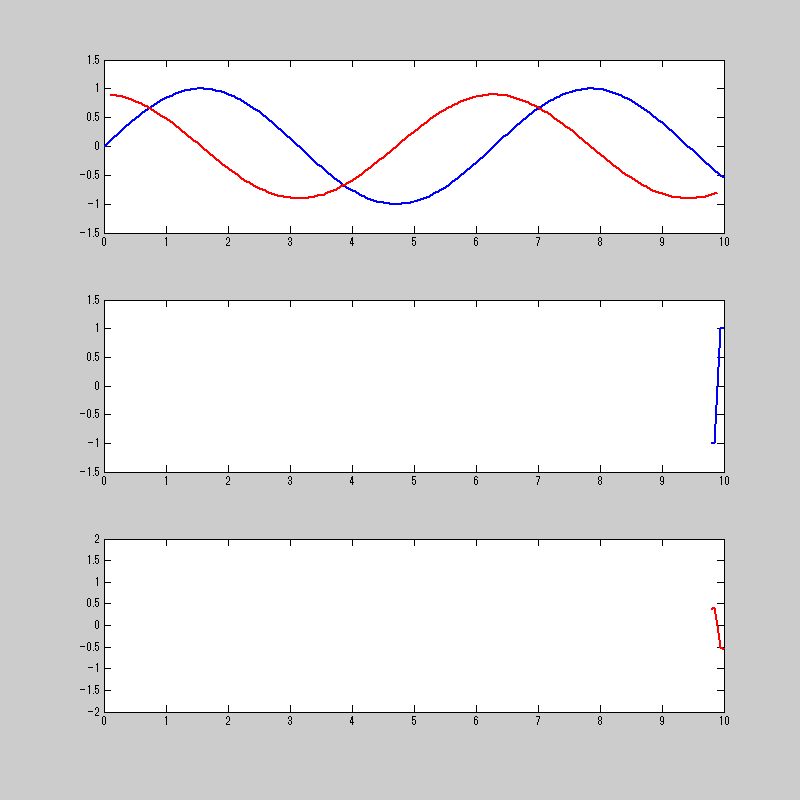

sin関数がcos関数になってるから、微分ができてる!!

注意点としては、あくまで微分相当であり、微分そのものではないってところだな。
さっきの画像は、微分っぽさを強調するため、畳み込みの結果にある程度のゲインを掛けてる。
欲しいのは、微分の変化が大きい部分を強調という性質なので、これでも十分と言える。

なるほど。
発想としては微分なんだけど、微分そのものじゃなくて、強調できる機能が欲しいってだけだね。

あとは、これを離散的に解釈した場合とか、画像のような平面に適用する場合にどうするかを考える。
まとめ

まとめだよ。
- エッジ検出をするには、変化の大きさを強調できる微分が相性が良い。
- だからといって導関数を求める必要はない。
- tanh関数で畳み込み積分をすると微分相当の結果が得られる。
- あくまで微分相当であり、微分の結果そのものではない。
- 欲しいのは変化の強調であるため、問題無い。
バックナンバーはこちら。




コメント