バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
畳み込み演算のガウシアンフィルタの話。
今回は2次ガウス分布関数について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
今回の範囲

ガウシアンフィルタ関連のやることリストを再掲
- 畳み込み演算
- 畳み込み積分
- 2次ガウス分布関数
- 良く使われるガウス分布カーネル
- 実際にガウシアンフィルタをやってみる

今回は2次ガウス分布関数?

そうそう。
2次ガウス分布関数

で、2次ガウス分布関数って何?

前回の1次元の畳み込み積分を行ったときに使用したのが1次ガウス分布関数。

あー、あの山なりな感じになってた関数か。

それの2次元版だね。
数式で書くとこんな感じ。
ちなみに\(\sigma\)は標準偏差だ。
\(
\displaystyle g(x,y,\sigma)=\frac{1}{\sqrt{2\pi\sigma}}\exp \bigg(-\frac{x^2+y^2}{2\sigma^2}\bigg)
\)

数式を見せられただけで、僕が理解できると思うなよ・・・。

(まぁ、そうだろうな・・・)
2次ガウス分布関数を図で書くと?

とりえあず、2次ガウス分布の3×3と5×5の場合の具体的数値とそれをグラフにしたものを載せておこう。
要は中心に重みが寄ってる山の形の関数ってことだな。
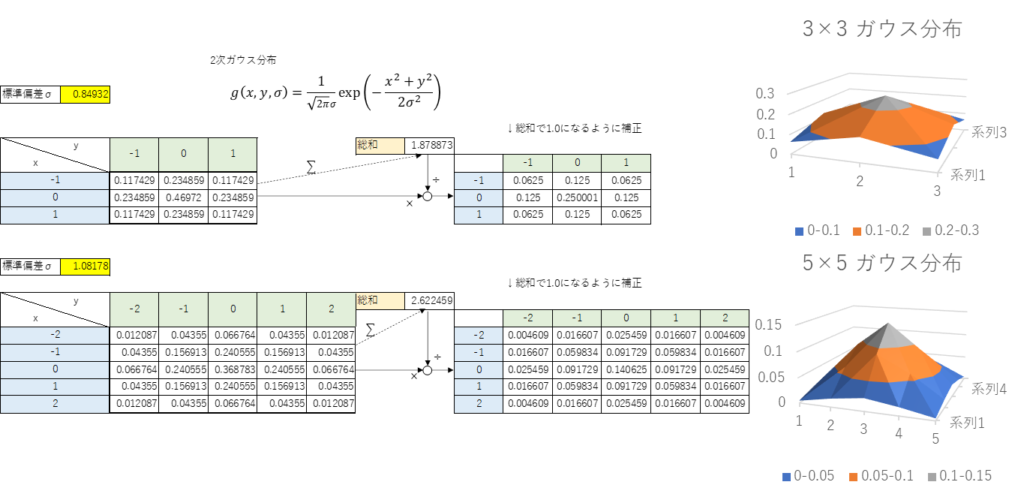

そうだよ!
こういうのでいいんだよ!

(孤独のグルメか・・・)

でもなんか、総和を出したあとに、それで全体を割ってるね?
これは何をしているの?

総和が1.0になるように補正を掛けてる。

なんで補正を掛けてるの?

総和が1.0になっていないと、畳み込み積分をした際に、元信号より増幅したり減衰したりする。
それを避けるための仕掛けだな。

なるほど。
しっかり考えられてるものってことか。
まとめ

まとめだよ。
- 2次ガウス分布関数について確認。
- 前回の畳み込み積分で使用した関数は1次ガウス分布関数。
- 数式で確認。
- 実施にグラフ表示で確認。
- 中心に重みが寄ってる山なりの関数。
- 元信号が増幅、減衰しないように、総和が1.0になるように細工するのが一般的。
バックナンバーはこちら。




コメント