バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia3-backnumber/
はじめに
畳み込み演算のガウシアンフィルタの話。
今回は畳み込み積分について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
今回の範囲

ガウシアンフィルタ関連のやることリストを再掲
- 畳み込み演算
- 畳み込み積分
- 2次ガウス分布関数
- 良く使われるガウス分布カーネル
- 実際にガウシアンフィルタをやってみる

今回は畳み込み積分?(なんか不穏な単語だ)
畳み込み積分

なんか、積分と付くと不穏な空気しか感じない・・・。

まぁ、厳密な定義までは掘り下げず、雰囲気だけ察してもらう感じだな。
これにより前回やった畳み込み演算の効能が分かる。
という想定だ。

結局、何をするものなの?畳み込み積分。

関数と関数を掛けた後に定積分。

(不穏どころの騒ぎじゃないよ・・・。)

やること自体は内積とほぼ一緒だな。
関数を、無限次元ベクトルと解釈した上での内積。
\(
\begin{bmatrix}
f_1 & f_2 & \dots & f_n
\end{bmatrix}
\begin{bmatrix}
g_1 \\ g_2 \\ \vdots \\ g_n
\end{bmatrix}\Delta t
\)

畳み込み演算も内積って言ってたから、どれもこれも結局は内積なのか。
畳み込み積分の効能

そして、畳み込み積分の効能だが、
ガウシアンフィルタを実施する上ではノイズ除去になる。
試しにアニメーションgifを作成してみた。
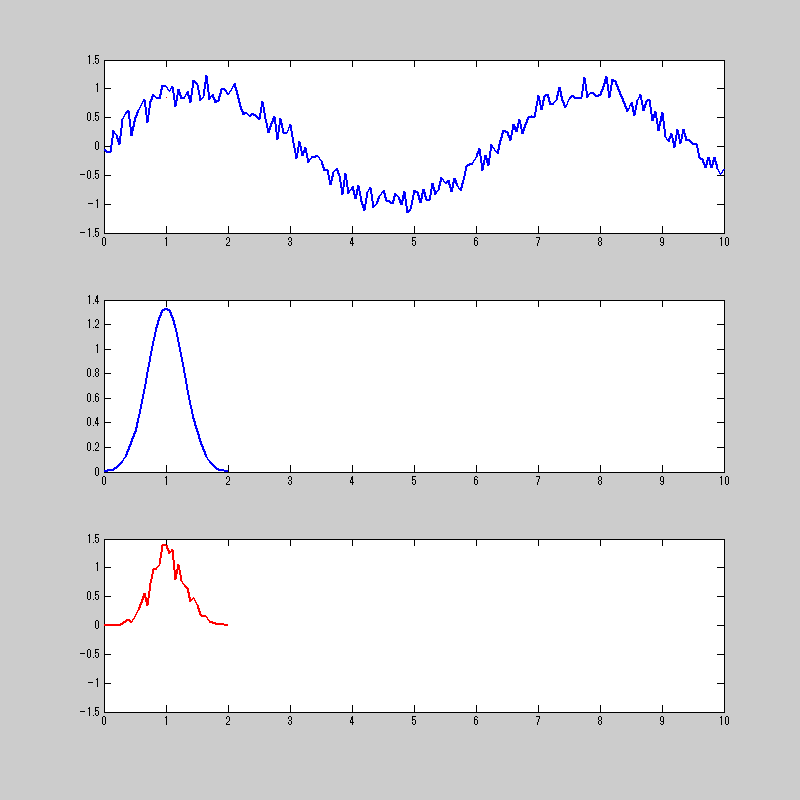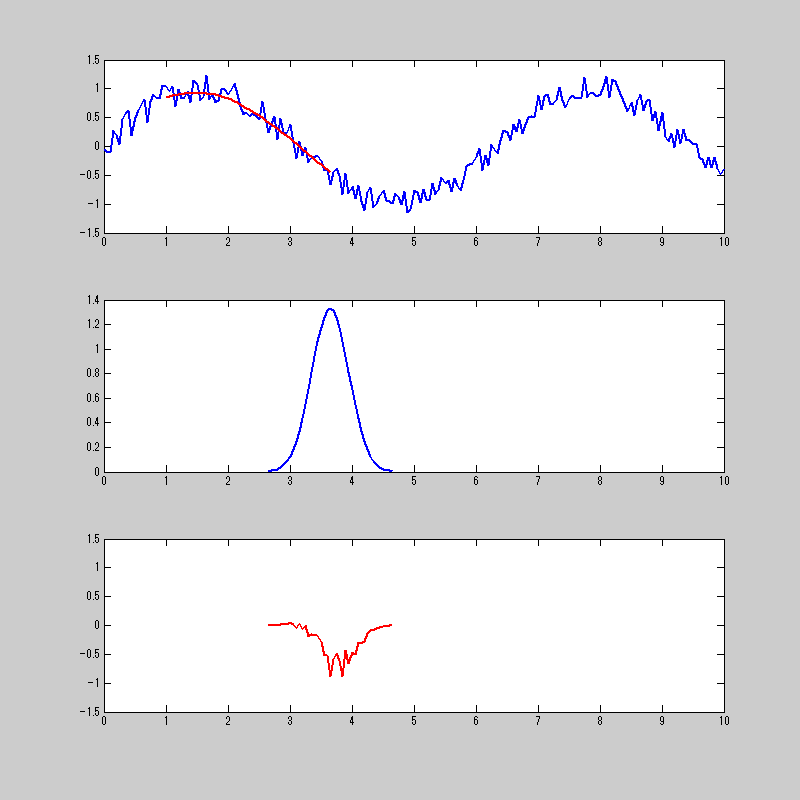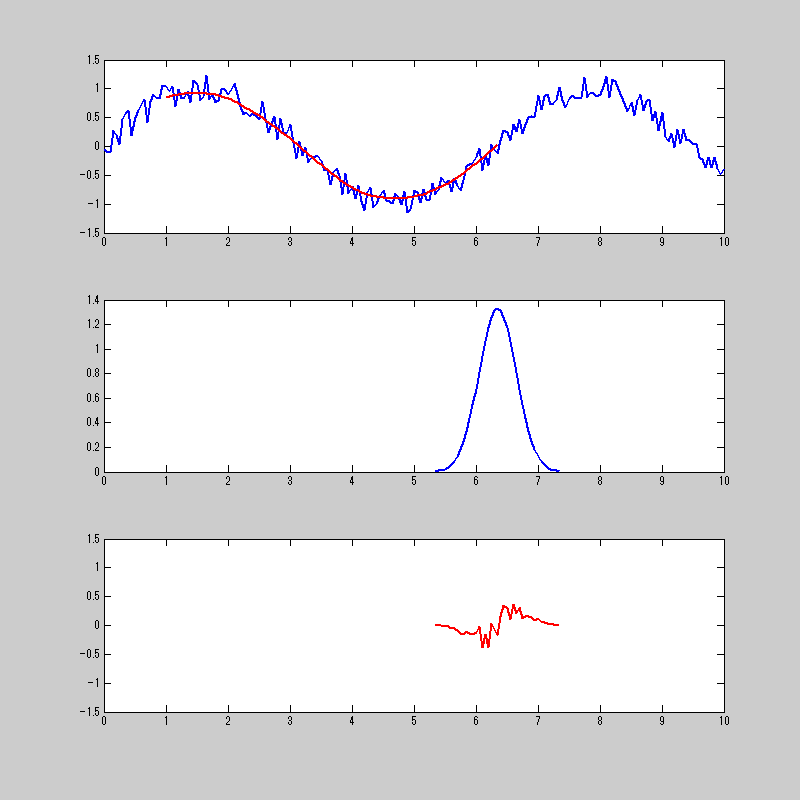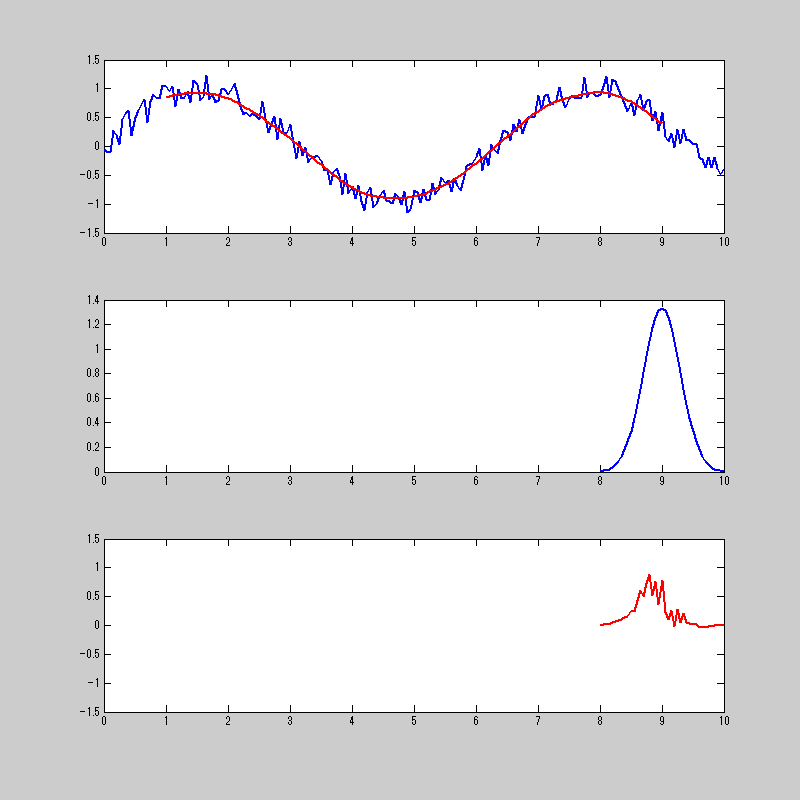

なんかミミズが暴れておる・・・。

一番上が、元の信号と畳み込み積分をした結果。
二番目が、畳み込み積分をする関数
三番目が、元信号の関数と畳み込みをする関数を掛け合わせたもの。
三番目の信号を合計したものが1番上の赤の信号になる。

これって、一番上のノイズが入った正弦波のノイズを除去してくれてるってことだよね?

そうそう。
これは1次元空間の信号に対して畳み込み積分を実施しているのを表しているものだが、
これを2次元空間の画像に対して行うのが畳み込み演算。
つまり、1次元、2次元の違いはあるけど、概念的には同一のものということになる。

なるほど。
確かにノイズ除去の効能のイメージは湧いてきたかも。
まとめ

まとめだよ。
- 畳み込み積分について超簡単に説明。
- 畳み込み積分の演算結果についてアニメーション。
- ノイズ除去の様子がわかる。
バックナンバーはこちら。




コメント