バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を用いた、多変量多項式回帰分析について。
今回は、Juliaで演算してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
正規方程式、各パラメータ、推定対象の多項式再掲

正規方程式と多変量多項式回帰分析で想定するパラメータの再掲だ。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
多項式回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1^2 & x_1y_1 & y_1^2 & y_1 &1\\
x_2^2 & x_2y_2 & y_2^2 & y_2 &1\\
\vdots & \vdots & \vdots\\
x_n^2 & x_ny_n & y_n^2 & y_n &1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta\\
\gamma\\
\delta\\
\epsilon\\
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
z_1\\
z_2\\
\vdots\\
z_n
\end{bmatrix}
\)
推定対象の多項式
\(
z=4x^2-5xy+3y^2+y+2
\)

これをJuliaで実現する。
Juliaコード

Juliaコードは以下になる。
using PyPlot
function meshgrid(xin,yin)
nx=length(xin)
ny=length(yin)
xout=zeros(ny,nx)
yout=zeros(ny,nx)
for jx=1:nx
for ix=1:ny
xout[ix,jx]=xin[jx]
yout[ix,jx]=yin[ix]
end
end
return (x=xout, y=yout)
end
n = 100
x = rand(n, 1)
y = rand(n, 1)
z = 4*x.^2 - 5*x.*y .+ 3*y.^2 + y .+ 2 + rand(n, 1) .-0.5
A=[x.^2 x.*y y.^2 y ones(length(x),1)];
b=z
X=(A'*A)^-1 *A'*b
print(X)
fig, (ax) = plt.subplots(1,
figsize=(8, 8),
subplot_kw=Dict("projection" => "3d"))
ax.scatter3D(x, y ,z)
xp=range(0, 1, length=5)
yp=range(0, 1, length=5)
xpm,ypm=meshgrid(xp,yp)
ax.plot_wireframe( xpm, ypm, X[1]*xpm.^2 + X[2]*xpm.*ypm + X[3]*ypm.^2 + X[4]*ypm .+ X[5])
ax.view_init(elev=20, azim=230)
plt.show()処理結果

処理結果は以下。
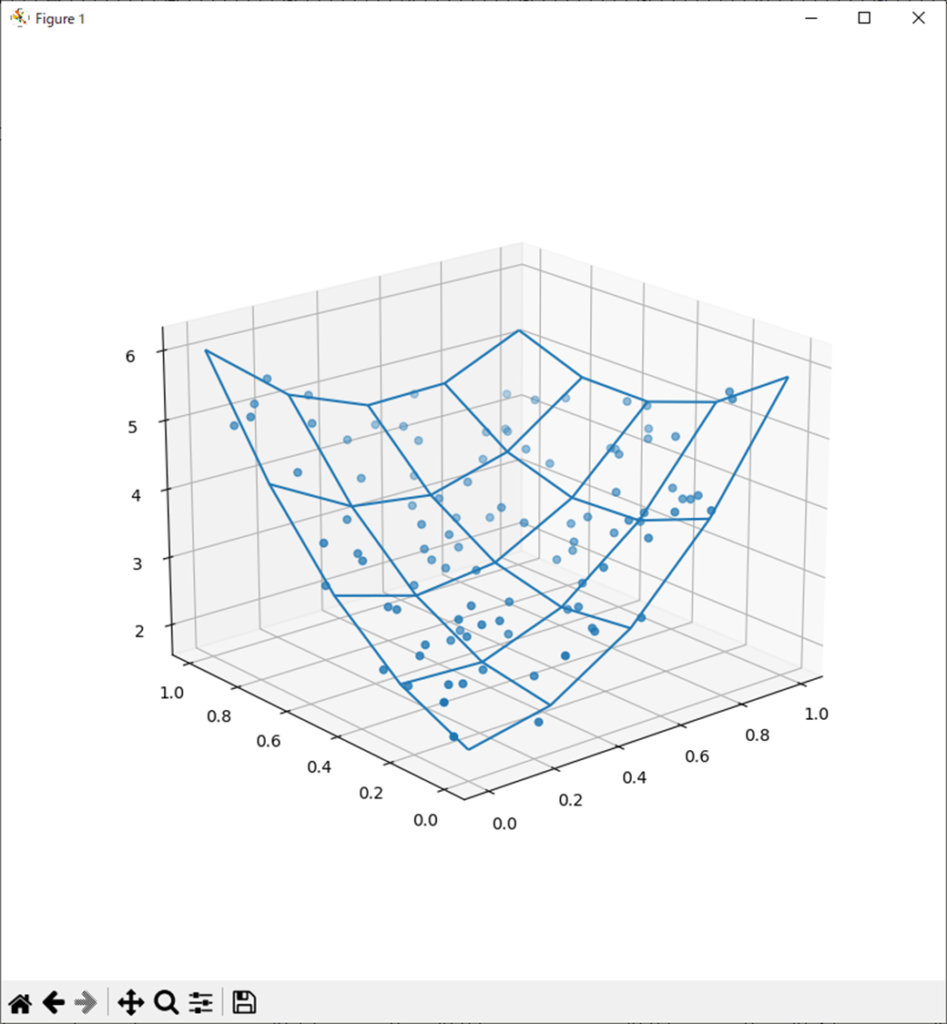
[3.877554790781497; -4.725063180237489; 2.886138352057935; 1.1512467219836287; 1.9884461731186933;;]考察

JuliaもMATLABのコピペで行ける・・・と思いきや、そうでもないな・・・。

演算部分はコピペだけど、グラフ表示がPython由来のmatplotlibベースだから、
その部分で乖離がある感じだな。

どっちにしても流れは一緒ってことか。

これ以外は特に特筆する話はないかな。
まとめ

まとめだよ。
- 正規方程式による多変量多項式回帰分析をJuliaで実施。
- 誤差はあるものの目的の係数の算出はできている。
- コード自体はMATLABコードのコピペ?
- 演算部分はコピペ。
- グラフ表示はmatplotlib仕様依存に書き方。
バックナンバーはこちら。




コメント