バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を用いた、多項式回帰分析について。
今回は、Scilabで演算してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
正規方程式、各パラメータ、推定対象の多項式再掲

まずは正規方程式、多項式回帰分析に於ける各パラメータ、推定対象の多項式の再掲。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
多項式回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1^2 & x_1 & 1\\
x_2^2 & x_2 & 1\\
\vdots & \vdots & \vdots\\
x_n^2 & x_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta\\
\gamma
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix}
\)
推定対象の多項式
\(
z=4x^2-5y+2
\)

これをScilabで解いてみる。
Scilabコード

Scilabコードは以下になる。
n = 100;
x = rand(1, n);
y = 4*x.^2-5*x+2+rand(1, n)-0.5;
A=[x'.^2 x' ones(length(x),1)];
b=y';
X=(A'*A)^-1 *A'*b;
disp(X);
plot(x, y ,'+');
xp=linspace(0, 1, 100);
yp=linspace(0, 1, 100);
plot( xp, X(1)*xp.^2+X(2)*xp+X(3), 'r','LineWidth',3);
処理結果

処理結果は以下。
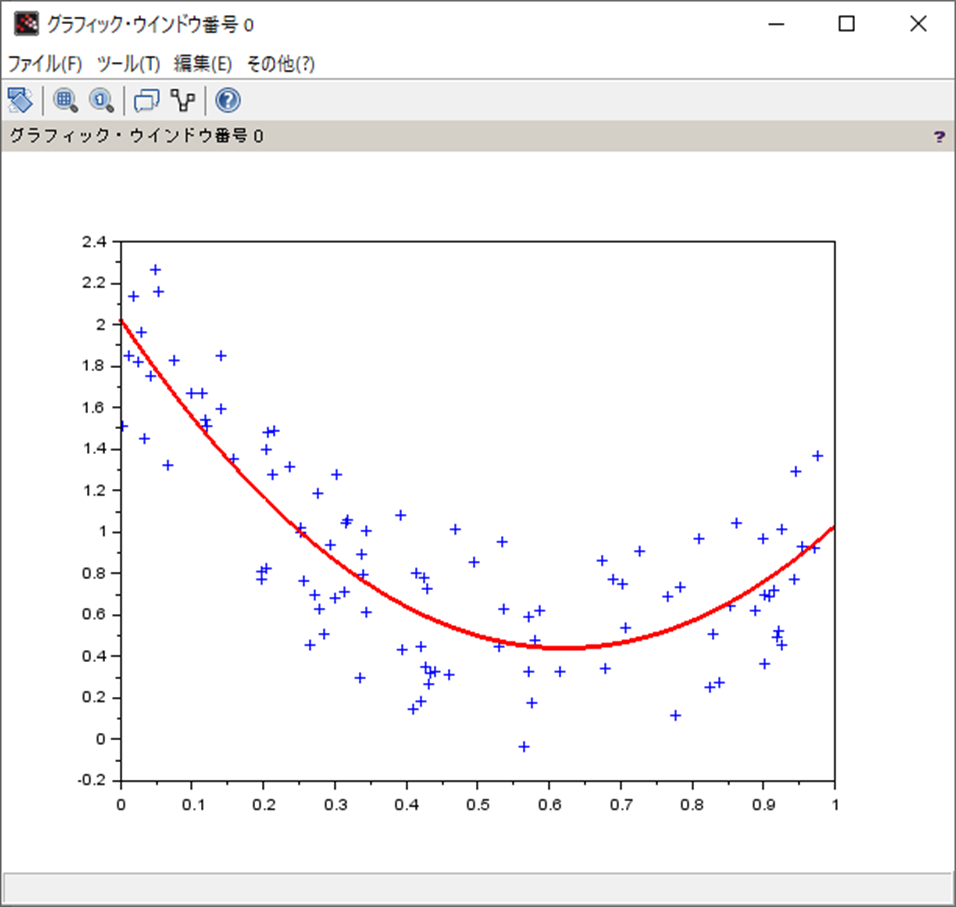
4.1096279
- 5.101752
2.0236114 考察

これもOK!

コード的にはMATLABと同一かな?

全く一緒だな。
だってコピペしただけだもん。

マジか!!

いままでもplotの微調整の部分に大きな差があって、演算部分には差がなかったし。
今回はplotの微調整がいらなかったんで、結果的に全く同一のコードになってしまったって感じ。

まさかコピペで行けるレベルで一緒とは・・・。
まとめ

まとめだよ。
- 正規方程式による多項式回帰分析をScilabで実施。
- 誤差はあるものの目的の係数の算出はできている。
- コード自体はMATLABコードのコピペで行けてしまった。
- plot部分の微調整が無かったんで。
バックナンバーはこちら。




コメント