バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を用いた、単回帰分析について。
今回は、Python(NumPy)で演算してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
正規方程式と各パラメータ再掲

まずは正規方程式と単回帰分析に於ける各パラメータの再掲。
正規方程式
\(
x=(A^TA)^{-1}A^Tb
\)
単回帰分析に於ける各パラメータ
\(
A=
\begin{bmatrix}
x_1 & 1\\
x_2 & 1\\
\vdots & \vdots\\
x_n & 1\\
\end{bmatrix},
\vec{x}=
\begin{bmatrix}
\alpha\\
\beta
\end{bmatrix},
\vec{b}=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix}
\)

今回は、これをPython(NumPy)を使用して解いてみる。
Pythonコード

Pythonコードは以下になる。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51])
y = np.array([10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40])
A=np.block([x.reshape(-1,1),np.ones((len(x),1))])
b=y.reshape(-1,1)
X=np.linalg.inv(A.T@A)@A.T@b
print(X)
xp = np.linspace(0, 4, 400)
plt.plot(x, y, '+', xp, X[0]*xp+X[1], '-' )
plt.ylim(10,41)
plt.xlim(0,4)
plt.show()処理結果

処理結果は以下。
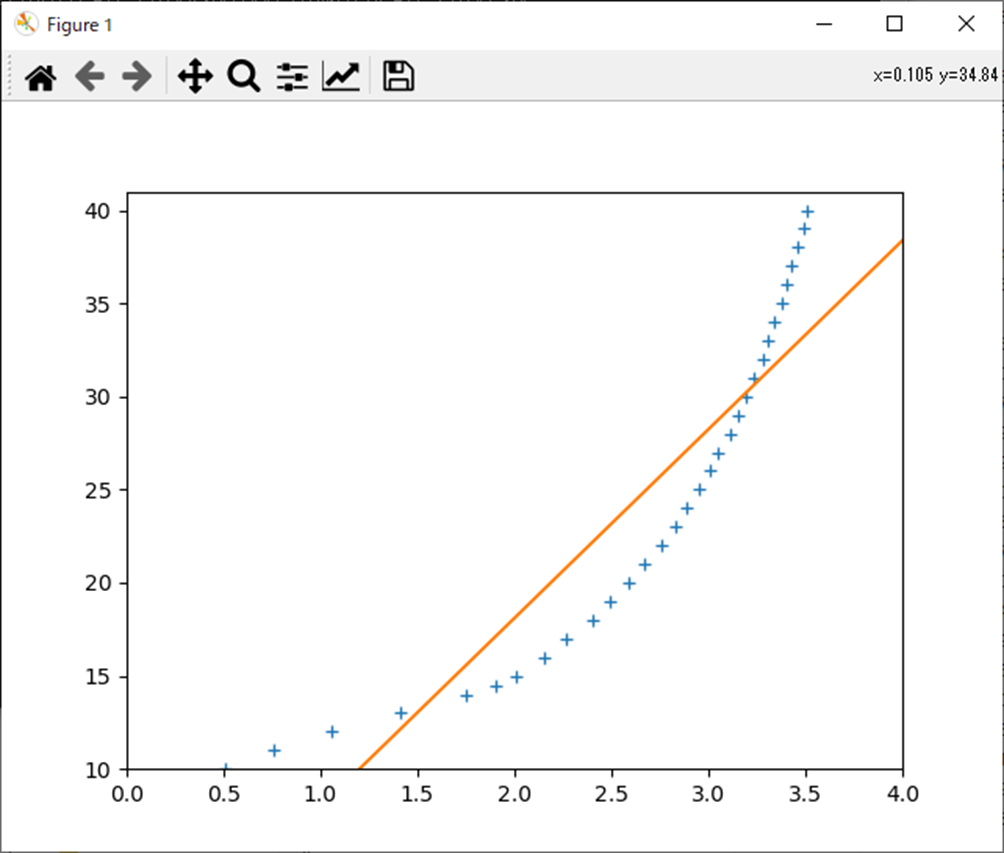
[[10.13303351]
[-2.16166437]]考察

結果としてはMATLABと一緒かな。
表示精度による差はあるけど。

同じ結果と見て良いだろう。

Pythonの内積は「@」だから、ここに注意が必要だね。

久しぶりにNumPyを使用したから、最初、間違って「*」で演算してしまった。
これだと内積でなく、アダマール積になってしまう。

ここは要注意だねー。
まとめ

まとめだよ。
- 正規方程式による単回帰分析をPython(NumPy)で実施。
- MATLABと同じ結果が得られた。
- ベクトル、行列の内積の演算子は「@」。
- 「*」にしてしまうとアダマール積になってしまうので注意。
バックナンバーはこちら。




コメント