バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を導出するまでの説明。
今回から、二乗和誤差の話になる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
ロードマップ【再掲】

今回は、二乗和誤差の話になる。
ロードマップで、位置づけを確認しておこう。

二乗和誤差

二乗和誤差ってなんか聞き覚えがあるんだよなー?

以前やった、最小二乗法の誤差関数だな。
ここらへんでやってる。

そっか。
正しいを思われる線との誤差を2乗にしたものを誤差関数として、この誤差関数を可能な限り小さくしたものが求めたい線。
って理屈だね。

そうそう。
で、今回やるのも理屈の上では全く一緒だ。
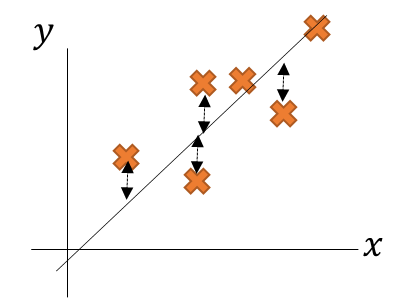

ちなみに一次関数の時の誤差関数こと二乗和誤差を再掲しておこう。
\(
\begin{eqnarray}
L(a,b)&=&\displaystyle\sum_{i=0}^n\{y_i -(ax_i +b)\}^2 \\
&=&\displaystyle a^2\sum x_i^2+nb^2+\sum y_i^2-2a\sum x_i y_i -2b\sum y_i +2ab\sum x_i
\end{eqnarray}
\)

確かにこんな感じだったね。
最小二乗法との差異

いっしょだったらもう別にやらなくてもOKだね。

理屈上一緒ってだけで同一とは言ってない。

え゛

まぁ、より一般化したものと言う感じだな。

一般化?
つまり簡単になったってこと?

数学の世界における一般化は、抽象度を引き上げて適用できる範囲を広げるって意味になるから、大体難しい方になるな。

だったらなんで一般化って、まるで簡単になるような言い回しをするんだ!?

いや、そういう言い方するってだけだから・・・。

今回の
どっちにしても、以前の最小二乗法の時の誤差関数は、
1変量1次関数を想定したものだった。
これを多変量にするのが、今回に於ける一般化だ。

いや、多変量と言われても・・・。

まぁそこは次回説明しよう。

嫌な予感しかしない・・・。
まとめ

まとめだよ。
- 二乗和誤差に関しては、以前の最小二乗法の誤差関数で扱ってはいる。
- 「正しいを思われる線との誤差を2乗にしたもの」という意味自体は変わらない。
- しかし、今回はこれを多変量として一般化しようという話になる。
バックナンバーはこちら。










コメント