バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を導出するまでの説明。
今回は二次形式の微分(勾配)を実際の多項式に適用したものをScilabで算出&プロットしてみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
ロードマップ&数式【再掲】

まずは恒例のロードマップと数式を再掲。

二次形式の多項式
\(
f(x,y)=3x^2+2y^2+5xy
\)
二次形式の多項式の偏導関数
\(
\displaystyle\frac{\partial f(x,y)}{\partial x}=6x+5y
\)
\(
\displaystyle\frac{\partial f(x,y)}{\partial y}=4y+5x
\)
二次形式の行列形式の偏導関数
\(
\nabla f(x,y) =
\begin{bmatrix}
\displaystyle\frac{\partial f(x,y)}{\partial x} \\
\displaystyle\frac{\partial f(x,y)}{\partial y}
\end{bmatrix}=
2AX=2
\begin{bmatrix}
3 & 5/2 \\
5/2 & 2
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix}
\)

今回はScilabで算出してみる。
Scilabコード

Scilabコードは以下になる。
a=3;
b=2;
c=5;
A=[a c/2; c/2 b];
N=6;
ax=linspace(0,10,N);
ay=linspace(0,10,N);
[x,y]=meshgrid(ax,ay);
polyY1=6*x+5*y;
polyY2=5*x+4*y;
subplot(2,2,1);
mesh(ax, ay, polyY1);
subplot(2,2,2);
mesh(ax, ay, polyY2);
X=[x(:)';y(:)'];
Y=2*A*X;
matY1=matrix(Y(1,:),N,N);
matY2=matrix(Y(2,:),N,N);
subplot(2,2,3);
mesh(ax, ay, matY1);
subplot(2,2,4);
mesh(ax, ay, matY2);
polyY1
polyY2
matY1
matY2処理結果

そして処理結果。
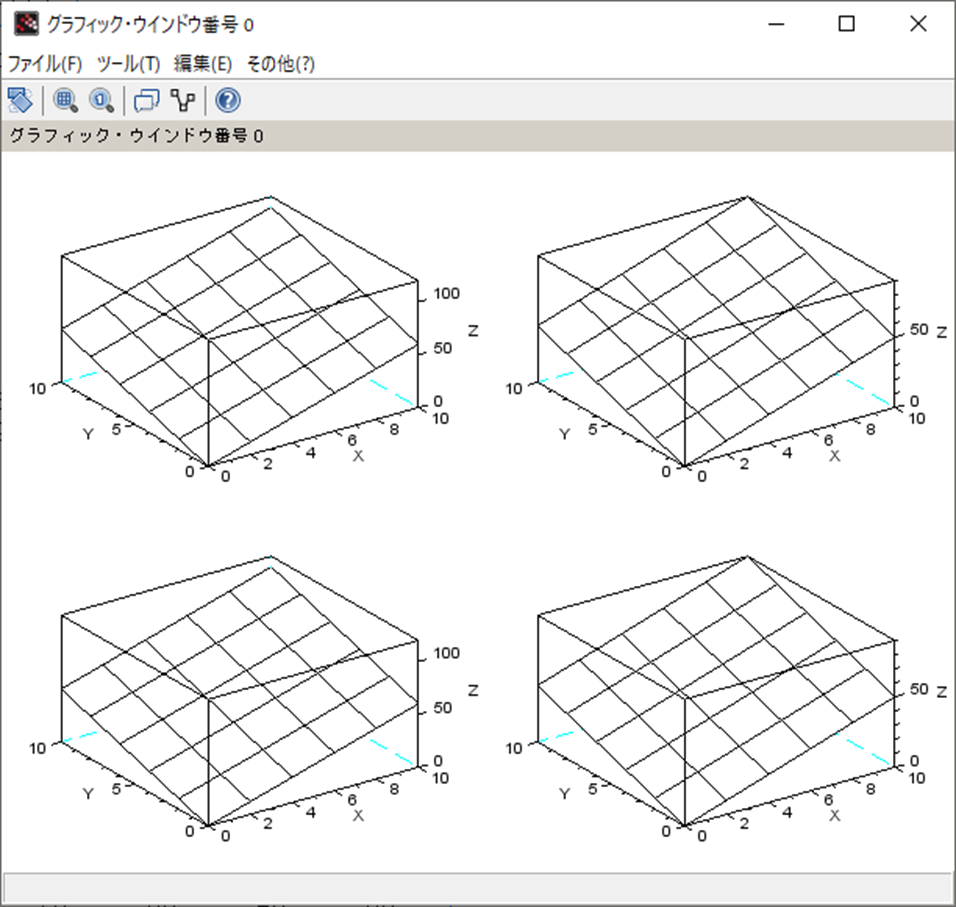
-->polyY1
polyY1 =
0. 12. 24. 36. 48. 60.
10. 22. 34. 46. 58. 70.
20. 32. 44. 56. 68. 80.
30. 42. 54. 66. 78. 90.
40. 52. 64. 76. 88. 100.
50. 62. 74. 86. 98. 110.
-->polyY2
polyY2 =
0. 10. 20. 30. 40. 50.
8. 18. 28. 38. 48. 58.
16. 26. 36. 46. 56. 66.
24. 34. 44. 54. 64. 74.
32. 42. 52. 62. 72. 82.
40. 50. 60. 70. 80. 90.
-->matY1
matY1 =
0. 12. 24. 36. 48. 60.
10. 22. 34. 46. 58. 70.
20. 32. 44. 56. 68. 80.
30. 42. 54. 66. 78. 90.
40. 52. 64. 76. 88. 100.
50. 62. 74. 86. 98. 110.
-->matY2
matY2 =
0. 10. 20. 30. 40. 50.
8. 18. 28. 38. 48. 58.
16. 26. 36. 46. 56. 66.
24. 34. 44. 54. 64. 74.
32. 42. 52. 62. 72. 82.
40. 50. 60. 70. 80. 90. 考察

これも結果としてはMATLABと同じく完全一致か。

コード自体もreshapeがmatrixになった程度であとはMATLABと一緒だ。
まとめ

まとめだよ。
- 二次形式の多項式としての偏導関数、行列形式による偏導関数を元にScilabで算出及びプロット。
- ともに同一の算出結果とプロットが得られた。
- コードの差はreshapeがmatrixになった程度。
バックナンバーはこちら。




コメント