バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を導出するまでの説明。
今回は二次形式の多項式表現と行列表現の計算をMATLABで実施する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
ロードマップおよび数式【再掲】

現在の場所としては二次形式。


MATLABで二次形式の多項式表現と行列表現の計算をしてみる回だね。

そして、行列表現の数式も再掲しておく。
\(
x^TA\circ x^T
\begin{bmatrix}
1\\
\vdots\\
1
\end{bmatrix}
\)

この数式に対して、多項式表現と行列表現の計算をしてみることになる。
\(
3x^2+2y^2+5xy
\)
MATLABコード

MATLABコードは以下になる。
a=3;
b=2;
c=5;
A=[a c/2; c/2 b];
N=6;
ax=linspace(0,10,N);
ay=linspace(0,10,N);
[x,y]=meshgrid(ax,ay);
subplot(2,1,1);
polyY=a.*x.^2+b.*y.^2+c.*x.*y;
mesh(ax, ay, polyY);
X=[x(:)';y(:)'];
Y=X'*A.*X'*ones(2,1);;
matY=reshape(Y,N,N);
subplot(2,1,2);
mesh(ax, ay, matY);
polyY
matY実行結果

実行結果は以下となる。
polyY =
0 12 48 108 192 300
8 40 96 176 280 408
32 84 160 260 384 532
72 144 240 360 504 672
128 220 336 476 640 828
200 312 448 608 792 1000
matY =
0 12 48 108 192 300
8 40 96 176 280 408
32 84 160 260 384 532
72 144 240 360 504 672
128 220 336 476 640 828
200 312 448 608 792 1000考察

まぁ数式通りに計算したってことだね。
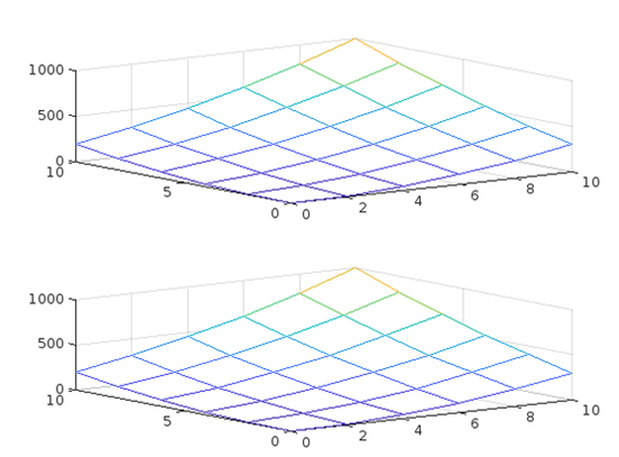
二次形式の多項式表現、行列表現で同じ結果になったのもわかる。

入力が\(x,y\)のに変数だから、meshgridで平面座標を生成してる感じか。

そうそう。

meshgridはx軸とy軸を入力すると、その範囲に於いての平面座標を生成してくれる。

3次元グラフはmeshという関数で実現してる感じか。
さほど手間がかかる感じではないね。

この手の処理はMATLABが一番癖が無くて扱いやすいな。
まとめ

まとめだよ。
- 二次形式の多項式表現と行列表現の計算をMATLABで実施。
- meshgridにx軸とy軸を入力とすることで平面座標が得られる。
- 平面座標を元に2変数の演算を実施。
- 演算結果をmesh関数を使用して3Dグラフに表示。
バックナンバーはこちら。




コメント