バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
正規方程式を導出するまでの説明。
今回は対称行列について。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
ロードマップ【再掲】

前回見せたロードマップを再掲しておこう。
この中の対称行列が今回の説明範囲だ。


毎回こんな感じで確認していくと、今どこら辺をやってるかわかりやすいね。
対称行列

で、今回は対称行列ってことだけど、
名前的に左右対称な行列ってことかな?

対称は対称なんだけど、
左右対称ではないな。

じゃー、どう対称なのさー。

対角に対して対称だな。

対角?

3×3の正方行列で表現するとこんな感じになるな。
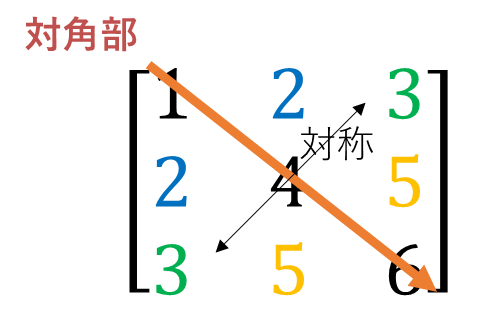

なるほど、左上から右下へ斜め方向の要素を指して対角っていうのか。

あと、当然ではあるけど、必ず正方行列だな。

とすると、単位行列も対称行列?

そうだね。
対称行列の対角部以外が0になっているものを対角行列と言うのだけど、
その対角行列の対角部が1になっているものを指す。

対角行列という新しい用語がぶっこまれたが、まぁ対角部だけに数値が入っているようなものか・・・。
対称行列の性質

そして対称行列の性質を説明しておこう。

これは当たり前と言えば当たり前なのだが、
転置しても値が変化しない。

そうなの?

これを見ればわかると思う。
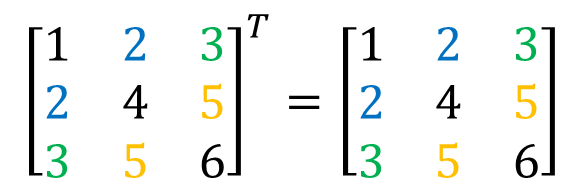

あ、なるほど。
確かにこれは転置しても変化しないね。
言われてみれば当たり前か。
対称行列がどこで生きてくるのか?

で、この対称行列ってどこで使うの?

次回からやっていく予定の
二次形式、二次形式の微分、グラム行列で使うな。
よって、まずは対称行列というものの存在をしってもらうだけでOKだ。

確かに存在すら知らないと、何を説明してもらってるか分からなくなりそうだもんね。
まとめ

まとめだよ。
- 対称行列について説明。
- 対角部を中心に対象となっている正方行列。
- 単位行列も対称行列の一種ではある。
- 厳密には対称行列の一種である対角行列の一種が単位行列。
- 対称行列は二次形式、二次形式の微分、グラム行列で使用する予定。
バックナンバーはこちら。




コメント