バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
平均、分散、共分散を用いた1次関数最小二乗法の係数算出について。
MATLABを使用して算出してみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
数式再掲

じゃ、お待ちかねの実際に演算してみる回になる。

やっとか・・・。

まずはMATLABだよね?

そうそう。

そして、数式を再掲しておこう。
\(
\begin{eqnarray}
a&=&\frac{\sigma_{xy}}{\sigma_x^2}\\
b&=&\bar{y}-a\bar{x}
\end{eqnarray}
\)
MATLABコード

そして、MATLABコードは以下になる。
x=[0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
y=[10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
% 共分散利用
C=cov(x,y,1);
disp('共分散行列')
disp(C);
disp('分散');
fprintf('xの分散=%f\n',var(x,1));
fprintf('yの分散=%f\n',var(y,1));
% 1次関数最小二乗法
a=C(1,2)/var(x,1);
b=mean(y)-a*mean(x);
fprintf('各係数 %.15f,%.15f\n',a,b);
xp = linspace(0, 4, 400); % 同定した1次関数のx軸を生成
plot(x, y, '+', xp, a*xp+b, '-' );
ylim([10,41]);
xlim([0,4]);
実行結果

実行結果は以下。
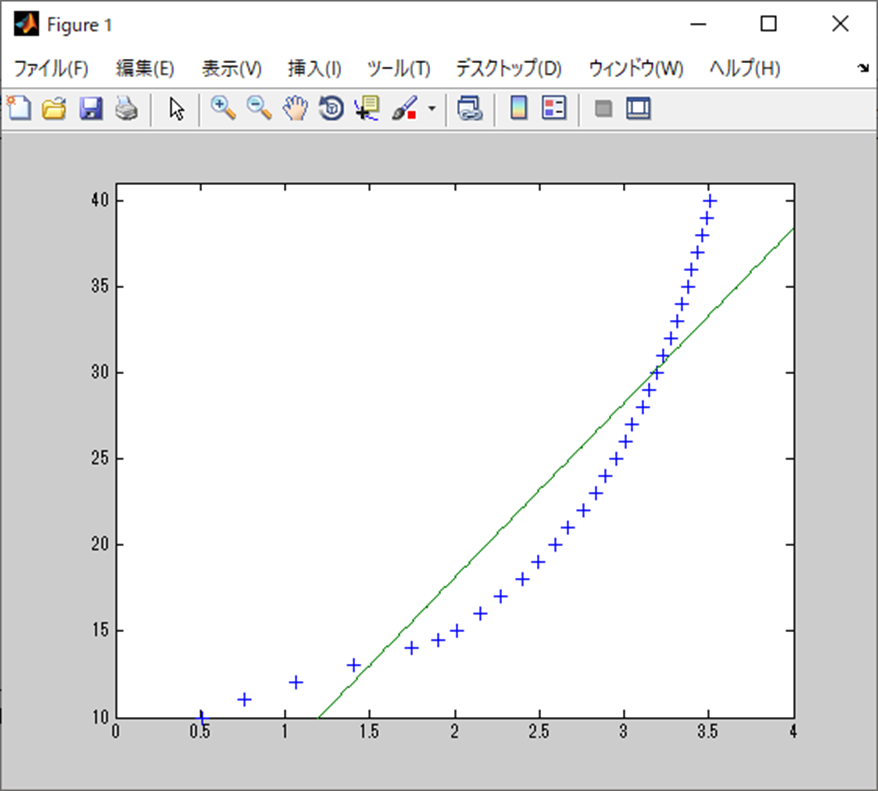
共分散行列
0.6616 6.7039
6.7039 80.8376
分散
xの分散=0.661590
yの分散=80.837646
各係数 10.133033511230931,-2.161664366928406考察

コードをみると、covって関数で共分散を取得してるみたいだね。
そして、varで分散を取得か。

引数に1ってのが追加されてるから、これで標本分散になってる感じかな?

そうだね。
共にデフォルトか0指定だと不偏分散になる。

あと、covの方って行列で返ってきてるよね?

covは共分散を返す関数というより、分散共分散行列を返す関数なんだよね。
構成は以下になる。
\(
\begin{bmatrix}
xの分散 && xyの共分散\\
yxの共分散 && yの分散
\end{bmatrix}
\)

ここにも分散が入ってるのか。

というわけで、実はvar関数を使わなくても分散は取得できる。
まぁ今回は明示的に分散を取得するということでvar関数使ったけど。

まぁこういうふうに返ってくるってのを知らないと共分散をうまく取得できないしね。
まとめ

まとめだよ。
- 平均分散共分散を使用した一次関数最小二乗法をMATLABで記載。
- covとvarを使用する。
- covは共分散だけでなく、分散共分散行列が取得される。
- よって、covだけでも分散は取得可能。
バックナンバーはこちら。




コメント