バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
平均、分散、共分散を用いた1次関数最小二乗法の係数算出について。
前回で数式としては導出できたが、
分散、共分散について一部説明しておく必要がある。
(不偏分散、不偏共分散)
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
不偏?標本?

さて、今回から実際にMATLABとかつかって計算してみるって感じだね。

ちょい待ち。

なに?(また妙な話ぶっこむ気だな・・・。)

実際にプログラムを組む際に
不偏分散、不偏共分散、標本分散、標本共分散の話にぶち当たる可能性が高い。

なんじゃそりゃー!!!
標本分散と不偏分散の数式比較

まず標本分散と不偏分散を数式で確認してみよう。
標本分散
\(
\displaystyle\sigma^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2
\)
不偏分散
\(
\displaystyle s^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2
\)

標本分散の方が僕がしってる分散だね。
不偏分散とは

でも、不偏分散ってなんだ?

まず、統計としては、
全データを対象とした記述統計と
母集団から一部をサンプルして、母集団を推定する推測統計に分かれる。

推測統計側は全データがそろってないけど、母集団を推測するには十分なデータがそろってる前提ってことだね。

そこで標本分散と不偏分散を見比べてると、
標本分散<不偏分散
となることがわかる。

\(\displaystyle \frac{1}{n}\)と\(\displaystyle \frac{1}{n-1}\)の差でそうなるね。

でもなんでこんなことを???

まぁ、推測統計に於いて、標本分散を行うと実際の分散より小さくなる傾向があるんだよ。
証明方法は割愛するが、以下のイメージになる。
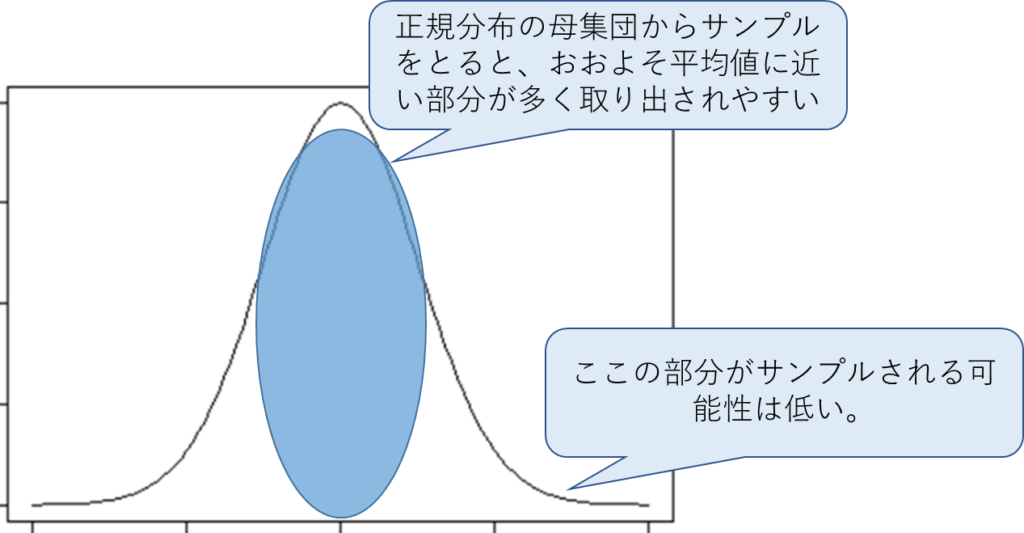

前提として母集団は正規分布に従うとしている。
ポイントは正規分布に対してサンプルをとると、平均値に近い部分からサンプルが取り出される可能性が高い点。
そうなると、分散はどうなるか?

母集団の分散より、サンプルした方の分散の方が小さくなる!

そのため、不偏分散ではやや大きくして、母集団の分散に近づけている。
\(\displaystyle \frac{1}{n}\)と\(\displaystyle \frac{1}{n-1}\)の\(n\)が大きくなれば、
両者の差を減っていくので、サンプル数が多くなると、標本分散でも母集団の分散に近付くのもわかるだろう。

こんな仕掛けがあったとは・・・。
なぜ不偏分散の話が出た?

で、なんで今回、不偏分散の話になったの?
どっち道、最小二乗法で使うのは標本分散の方でしょ?

各ツール、各言語で分散、共分散を計算してくれる関数があるんだけど、
大体がデフォルトで不偏分散を算出してくるんだよね。

え?!
欲しいのは標本分散なんだけど?!

一応、オプションを追加することで、標本分散を取得できることが多い。
だけど、標本分散、不偏分散の存在とその意味を理解してないとたぶん迷子になる。

それで事前に標本分散と不偏分散の話を出したわけか・・・。

まぁそういうった種類があることはわかったから、
そこに気を付けながら各ツール、各言語を使えばOKだね。
共分散の方

理屈は一緒だが、
共分散も母集団全体か標本かで2パターンになる。
これも各ツール、各言語の関数で得られるがオプションでの切り替えが必要になるだろう。
標本共分散
\(
\displaystyle \sigma_{xy}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})
\)
不偏共分散
\(
\displaystyle s_{xy}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})
\)
まとめ

まとめだよ。
- 標本分散と不偏分散について説明。
- 証明方法は割愛。
- 図を見て、不偏分散の必要性を察っするレベルで確認。
- 各ツール、各言語で分散を求める関数等があるが、大体が不偏分散。
- オプション指定で標本分散にすることも恐らく可能。
バックナンバーはこちら。




コメント