バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
平均、分散、共分散を用いた1次関数最小二乗法の係数算出について。
いままで導出してきた変形式を組み合わせてみる。
今回は係数\(a\)を求めるのがメイン。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
いままで導出してきた数式たち【再掲】

前回は係数\(b\)を求めたが、
その続きとして今回は係数\(a\)を求める。
まずは使用する数式たちを再掲しておこう。
\(
\begin{eqnarray}
\displaystyle a\sum 1 &=& an \dots 総和の変形 \\
\displaystyle n\bar{y}&=&\sum y_i \dots 平均の変形 \\
\displaystyle \sigma_x^2 &=&\bar{x_i^2}-(\bar{x})^2 \dots 分散の変形 \\
\displaystyle \sigma_{xy}&=&\frac{1}{n}\sum x_i y_i – \bar{x}\bar{y} \dots 共分散の変形
\end{eqnarray}
\)
1次関数最小二乗法を求めるための連立方程式
\(
\begin{eqnarray}
\displaystyle a\sum x_i^2 + b\sum x_i &=& \sum x_i y_i \dots (1)\\
\displaystyle a\sum x_i + b\sum 1 &=& \sum y_i \dots (2)
\end{eqnarray}
\)
前回求めた係数\(b\)を求める式
\(
b=\bar{y}-a\bar{x}
\)

係数\(b\)を(1)に代入すれば、係数\(a\)が求まるはず。
って感じだね。

そうそう。
係数aを求める

以下が導出過程になる。
平均、平均の変形、分散の変形、共分散の変形を利用する。
\(
\begin{eqnarray}
\displaystyle a\sum x_i^2+b\sum x_i &=&\sum x_i y_i \\
-\sum x_i y_i+a\sum x_i^2+b\sum x_i &=& 0 \\
\end{eqnarray}
\)
ここで\(b\)を代入
\(
\begin{eqnarray}
\displaystyle -\sum x_i y_i+a\sum x_i^2+(\bar{y}-a\bar{x})\sum x_i &=& 0 \\
-\sum x_i y_i+a\sum x_i^2+\bar{y}\sum x_i-a\bar{x}\sum x_i &=& 0
\end{eqnarray}
\)
\(\displaystyle\sum x_i\)を\(n\bar{x}\)に置き換え、両辺をマイナスする。
\(
\begin{eqnarray}
\displaystyle \sum x_i y_i-n\bar{y}\bar{x}-a(\sum x_i^2-n\bar{x}\bar{x})&=&0 \\
n(\frac{1}{n}\sum x_i y_i-bar{y}\bar{x})-an(\frac{1}{n}\sum x_i^2-(\bar{x})^2)&=&0 \\
n(\frac{1}{n}\sum x_i y_i-bar{y}\bar{x})-an(\bar{x_i^2}-(\bar{x})^2)&=&0 \\
n\sigma_{xy}-an\sigma_x^2&=&0 \\
a&=&\frac{\sigma_{xy}}{\sigma_x^2} \qquad //
\end{eqnarray}
\)
傾きはこと係数aは共分散/分散?

むっちゃシンプルな式になったーーー!!!

ホントにあってるの?

計算上はあってるな。
まぁ共分散と分散を計算式を元に図解してみよう。
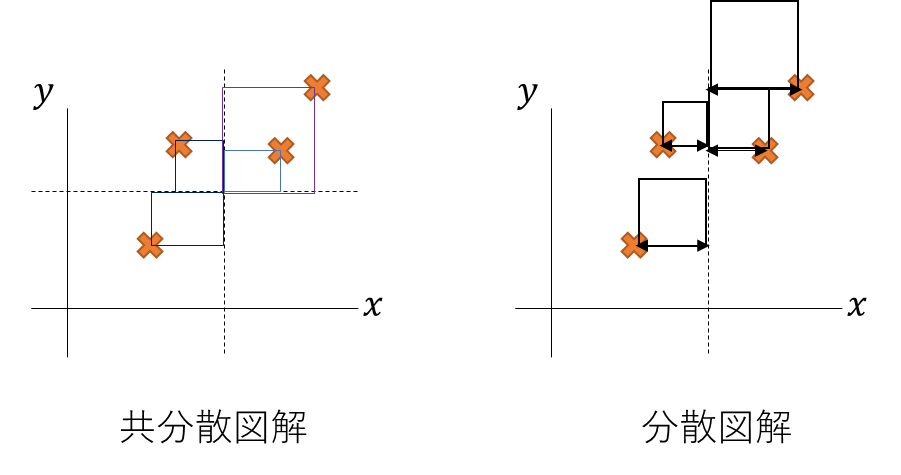

×印がサンプルした値で
それに対して、真値から見た共分散と分散の値を四角形の面積で示しているとみてほしい。
共分散は真値からのx,y方向の差を掛けた四角形の面積。
分散は、x方向のみの差を掛けた四角形の面積。
つまり共分散/分散に於いての四角の面積比としてはy/xが成立しそう。つまり傾きが求まる。

ここで言ってる真値ってのは、最小二乗法で求めた式から算出される値ってこと?

そうそう。
こらから求めるはずのものが仮置きされてると思えば良い。

細かいところは理解できてないけど、四角形の面積から考えると、共分散/分散は確かに傾きっぽいなー。

こんな感じで、数式としても、感覚としても正しいってことだな。

まぁ両方の観点からの確かさってのはわかるってのは重要だよね。

というわけ、次回からは実際にこの数式を使用して1次関数最小二乗法をやってみる。
まとめ

- 平均、平均の変形、分散の変形、共分散の変形を用いて係数aを求めた。
- 共分散、分散の計算式を元に図解すると四角形の面積で表現できる。
- x,y方向の差の積による四角形、x方向の差の二乗による四角形の比なので、傾きを求めるのと同一となる。
バックナンバーはこちら。




コメント