バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
平均、分散、共分散を用いた1次関数最小二乗法の係数算出について。
今回は、共分散の定義及び変形式の確認する。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
共分散

流れ的には、今回は共分散の話になるのだろうけど、
そもそも共分散ってのが何者か知らないんだよねー。

確かに共分散は分かりにくい概念だな。
まずはWikipediaを引用しよう。
共分散(きょうぶんさん、英: covariance)とは、大きさが同じ2つのデータの間での、平均からの偏差の積の平均値である
Wikipediaより(https://ja.wikipedia.org/wiki/%E5%85%B1%E5%88%86%E6%95%A3)

これだけで何を察しろと・・・。

そのWikipediaに例が載ってるだけど、それを見た方が良いかもね。
2つのデータの相関性を評価するためのものと思えばOKだよ。
共分散の性質
- 0ならば2つのデータの間に相関は無い
- 正ならば、2つのデータの間に正の相関があり、値が大きい方がより強い相関になる。
- 負ならば、2つのデータの間に負の相関があり、値が大きい方がより強い相関になる。
相関

正の相関、負の相関と言われても・・・。

ざっと書くとこんな感じだな。
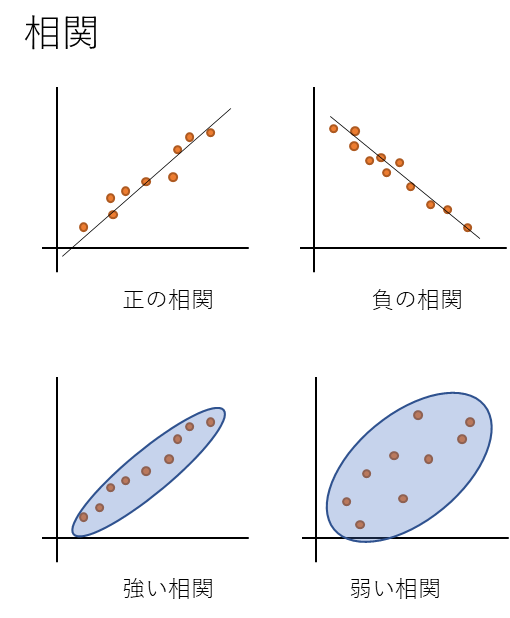

あ、なるほど。
こういう状態を言うのか。
確かに、こういう図を見ると最小二乗法との関係性は感じるね。
共分散の基本公式と変形式

じゃ、一気に共分散の共分散の基本公式と変形式を出そう。
これも最後の変形式が重要な式となる。
\(
\begin{eqnarray}
\displaystyle \sigma_{xy}&=&\frac{1}{n}\sum(x_i-\bar{x})(y_i-\bar{y})\dots基本公式 \\
&=&\frac{1}{n}\sum(x_i y_i-\bar{x}y_i-x_i\bar{y}+\bar{x}\bar{y}) \\
&=&\frac{1}{n}\sum x_i y_i – \frac{\bar{x}}{n}\sum y_i – \frac{\bar{y}}{n}\sum x_i+\frac{\bar{x}\bar{y}}{n}\sum 1\\
&=&\frac{1}{n}\sum x_i y_i – \bar{x}{\color{red}{\frac{1}{n}\sum y_i}} – \bar{y}{\color{red}{\frac{1}{n}\sum x_i}}+\bar{x}\bar{y}{\color{red}{\frac{1}{n}\sum 1}}\\
&=&\frac{1}{n}\sum x_i y_i – \bar{x}\bar{y}-\bar{y}\bar{x}+\bar{x}\bar{y}\\
&=&\frac{1}{n}\sum x_i y_i – \bar{x}\bar{y}
\end{eqnarray}
\)

これもごちゃごちゃいろいろこねくり回した割には異様にシンプルになったなぁ。

ポイントは赤文字にしている部分だな。
これは平均の公式と一緒だ。

あ!ほんとだ!だから、その後ろの式で平均と置き換えてシンプルになるように変形できたのか!

そうそう。
これで、1次関数の最小二乗法に対する変形の準備が整ったところだ。
まとめ

まとめだよ。
- 共分散について簡単に説明。
- 2種類のデータの相関性を評価できる。
- 相関性について簡単に説明。
- 正の相関、負の相関。
- 強い相関、弱い相関。
- 共分散の式を変形した。
バックナンバーはこちら。




コメント