バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
1次関数最小二乗法の係数算出の式をPython(Numpy)を使用して実現。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
1次関数最小二乗法 算出式【再掲】

まずは 係数算出式の再掲だ。
\(a,b\)を逆行列で算出
\(
\begin{bmatrix}
a \\
b
\end{bmatrix}=
\begin{bmatrix}
\sum x_i^2 && \sum x_i \\
\sum x_i && \sum 1
\end{bmatrix}^{-1}
\begin{bmatrix}
\sum x_i y_i \\
\sum y_i
\end{bmatrix}
\)
\(a,b\)を\(\sum\)で算出
\(
\begin{eqnarray}
\displaystyle a&=&\frac{n\sum x_i y_i – \sum x_i \sum y_i}{n\sum x_i^2 – (\sum x_i)^2} \\
\displaystyle b&=&\frac{-\sum x_i \sum x_i y_i + \sum x_i^2 \sum y_i}{n\sum x_i^2 – (\sum x_i)^2}
\end{eqnarray}
\)

これを今回はPython(Numpy)でやるとどうなるかって話か。

そうそう。
Pythonコード

Pythonコードは以下になる。
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51])
y = np.array([10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40])
print("Σで計算")
n = len(x)
denominator = n*sum(x**2)-sum(x)**2
a=(n*sum(x*y)-sum(x)*sum(y))/denominator
print("a=", a )
b=(-sum(x)*sum(x*y)+sum(x**2)*sum(y))/denominator
print("b=", b )
print("行列計算")
V_ab = np.linalg.inv(np.array([[sum(x**2),sum(x)],[sum(x),n]]))@np.array([sum(x*y),sum(y)])
print(V_ab)
xp = np.linspace(0, 4, 400) # 同定した1次関数のx軸を生成
plt.plot(x, y, '+', xp, a*xp+b, '-' )
plt.ylim(10,41)
plt.xlim(0,4)
plt.show()結果

結果は以下になる。
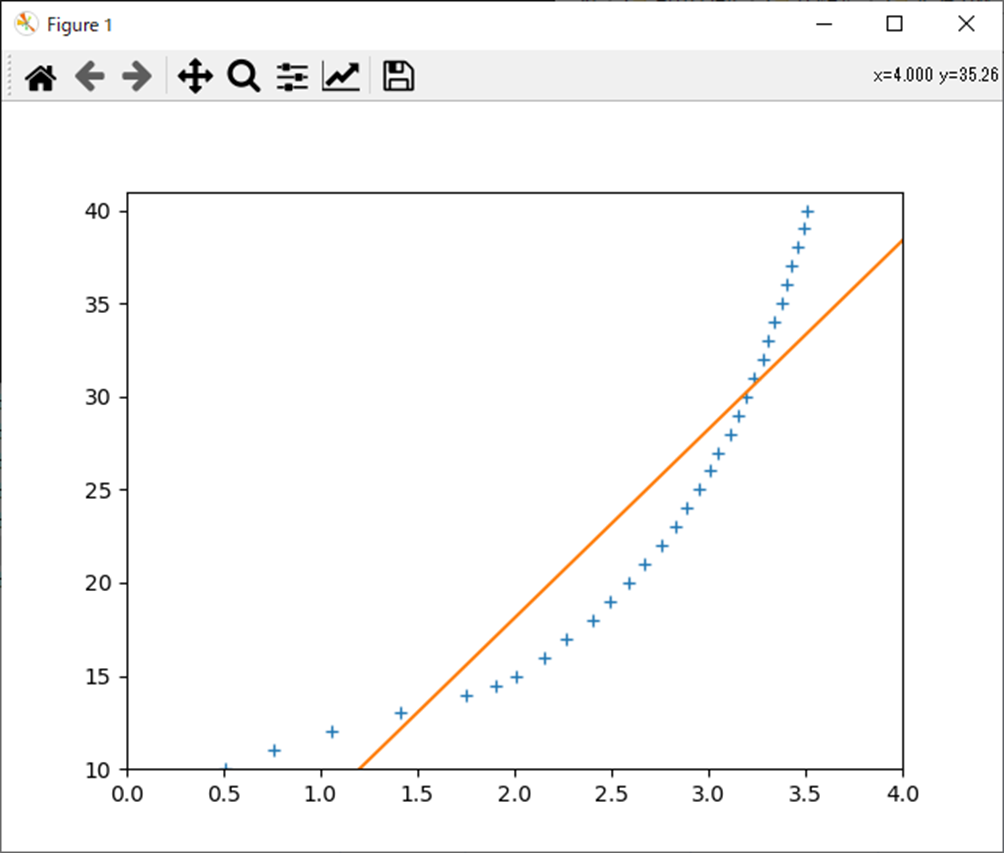
Σで計算
a= 10.133033511230964
b= -2.1616643669284774
行列計算
[10.13303351 -2.16166437]
これもnp.ployfitと同じ結果が得られたね。

まぁ算出するコンセプトは同じだろうからね。
演算誤差が載る程度の差しか出ないのだろう。
まとめ

まとめだよ。
- 1次関数最小二乗法の係数算出の式を元にPython(Numpy)で実装。
- np.polyfitと同じと解釈できる結果が得られた。
バックナンバーはこちら。




コメント