バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
1次関数最小二乗法の係数算出の式をMATLABを使用して実現。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
1次関数最小二乗法 算出式【再掲】

まずは以前導出した、1次関数最小二乗法の係数算出の式を再掲しておこう。
\(a,b\)を逆行列で算出
\(
\begin{bmatrix}
a \\
b
\end{bmatrix}=
\begin{bmatrix}
\sum x_i^2 && \sum x_i \\
\sum x_i && \sum 1
\end{bmatrix}^{-1}
\begin{bmatrix}
\sum x_i y_i \\
\sum y_i
\end{bmatrix}
\)
\(a,b\)を\(\sum\)で算出
\(
\begin{eqnarray}
\displaystyle a&=&\frac{n\sum x_i y_i – \sum x_i \sum y_i}{n\sum x_i^2 – (\sum x_i)^2} \\
\displaystyle b&=&\frac{-\sum x_i \sum x_i y_i + \sum x_i^2 \sum y_i}{n\sum x_i^2 – (\sum x_i)^2}
\end{eqnarray}
\)

そうそう。
逆行列で求めるパターンと、
それだけだと行列を扱えない環境で困るかもしれないから\(\sum\)で算出するパターンもやったんだった。

これを各ツール、各言語で実施する。

前回までは各ツール、各言語の最小二乗法を実現してくれるライブラリ的なものを使用したけど、
今回は、それは未使用ってことだね。

そうそう。
MATLABコード

まずはMATLABコード。
function y=LeastSquares_test()
x=[0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
y=[10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
% Σで計算
disp('Σで計算');
n = length(x);
denominator = n*sum(x.^2)-sum(x)^2;
a=(n*sum(x.*y)-sum(x)*sum(y))/denominator;
b=(-sum(x)*sum(x.*y)+sum(x.^2)*sum(y))/denominator;
s = sprintf('a=%f,b=%f\n', a,b);
disp(s);
% 行列計算
disp('行列計算');
V_ab = inv([sum(x.^2), sum(x) ; sum(x), n])*[sum(x.*y) ; sum(y)];
s = sprintf('a=%f,b=%f\n', V_ab(1),V_ab(2));
disp(s);
xp = linspace(0, 4, 400);
plot(x, y, '+', xp, a*xp+b, '-' );
ylim([10,41]);
xlim([0,4]);
end結果

結果は以下になる。
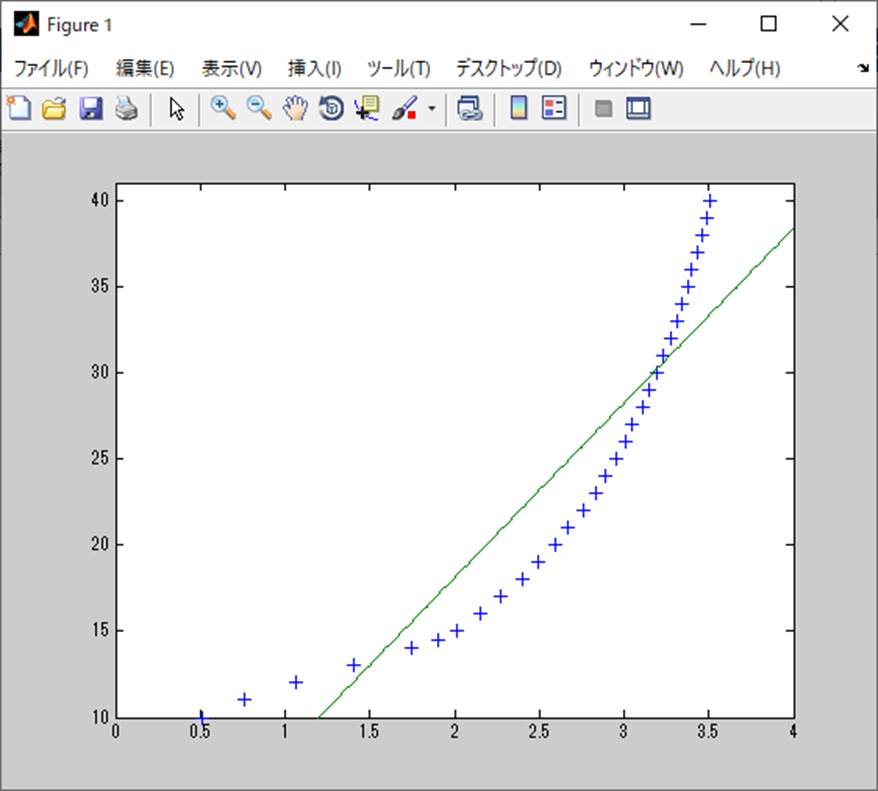
Σで計算
a=10.133034,b=-2.161664
行列計算
a=10.133034,b=-2.161664
これは同じ結果が得られたってことか。

そうだね。
まぁ同じアルゴリズムを使用しているわけだから、
演算誤差は別として、同一の結果は得られるだろう。

こういうふうに実現できると頑張って解説を聞いてきた甲斐があるってもんだね。
まとめ

まとめだよ。
- 1次関数最小二乗法の係数算出の式を元にMATLABで実装。
- polyfitと同じと解釈できる結果が得られた。
バックナンバーはこちら。




コメント