バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
最小二乗法をJuliaを使って解いてみる話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
Juliaによる1次関数の最小二乗法

今回はJuliaだが・・・。

Juliaが一番慣れてないから、どうなるかが読みずらい。

でも、一撃で解けるようなライブラリがあるんでしょ?

Polynomialsパッケージのfit関数が該当するな。

Polynomialsって確か多項式って名前で、
それのfit関数だから、
MATLAB,PythonのNumpyのpolyfitに近い表現だね。

ということは、MATLABと似た感じで行けるのか?!

まぁ似ていると言えば似ているが、根本的に異なってる部分もあるな。

え゛

まぁ今回に於いては大した問題ではないが、
取得できるのが係数じゃなくて関数になる。
まぁ関数そのものを参照できるから、係数の確認はできるけどね。
むしろ、今回の目的からすると関数のままplotに渡せばOKだから、楽になったと言えるかも。

なんか、いろいろ言ってるってことしかわからん。

まぁ見た方が早いな。
Juliaコード

Juliaコードは以下になる。
using Polynomials
using PyPlot
x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51];
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40];
func = fit(x, y,1);
print("各係数")
print(func)
xp=Vector(0:1/400:4);
plot(x, y, "+" );
plot(xp, func.(xp) );
ylim([10,41]);
xlim([0,4]);実行結果

実行結果は以下になる。
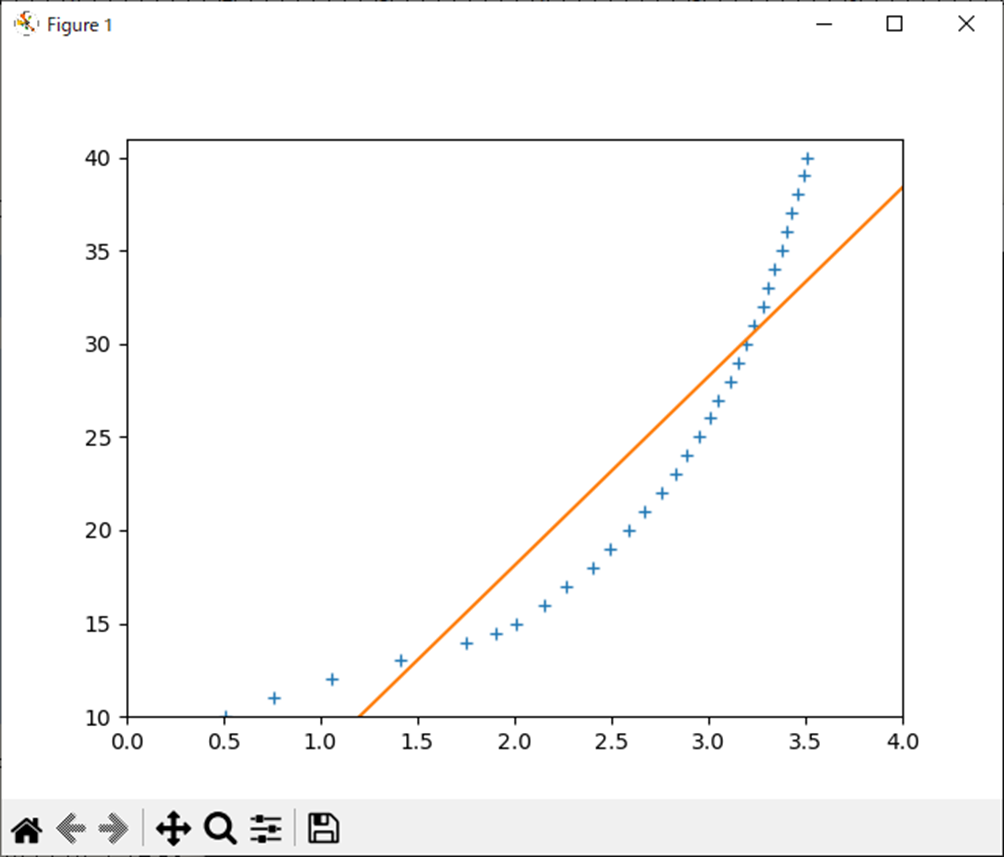
各係数
-2.16166 + 10.133*x
func = fit(x, y,1);
で最小二乗法を実施してるんだけど・・・。
戻りが関数なのか?!

だから、そう言ったじゃん。

でも、関数をprintすると係数が確認できるから、
今回の目的としては問題ないのか。
そして、関数をplotにそのまま渡せばOKと。

だから、そう言ったじゃん。

言われただけで理解出来たら苦労しないよ!

まぁ、それは分かる。

あと、係数単体の値が欲しい場合は以下のように取得できる。
julia> func[0]
-2.161664366928408
julia> func[1]
10.133033511230932
係数単体も取得できるんだったら、問題は起きなそうだね。
まとめ

まとめだよ。
- Juliaにて1次関数の最小二乗法を実施。
- Polynomialsパッケージのfit関数を使用。
- 他のツール、言語と異なり、係数ではなく、関数が取得される。
- 配列としてアクセスすれば、係数単体の値と取得できる。
バックナンバーはこちら。




コメント