バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
最小二乗法をScilabを使って解いてみる話。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
Scilabによる1次関数の最小二乗法

次はScilabだね。

Scilabは大体MATLABと似てること多いし、
PythonのNumpyも関数名はpolyfitだったから、きっとScilabも同じだね。

残念ながら違う。
使い方の雰囲気も違うな。

え゛

ここでは詳細説明は割愛するが、Scilabで使用する関数はlsq。
MATLAB、PythonのNumpyのpolyfitと比べると実は高機能。

ということは使い方も難しい???

まぁ難しい使い方もできるが、今回の1次関数を前提にした場合は、それほど難しくはない。
ただ、「なんでこんなパラメータなの?」という疑問は湧いてくるだろうね。
これはもっと複雑な多項式にも適用できるためのものではあるのだけど。

よくわからんけど、パラメータの渡し方次第ではもっとすごいことができるんだけど、
今回の1次関数を前提とすれば、それほど複雑にならない。
それでも、複雑さが隠し切れない部分があるって感じか。

その認識でOKだ。
Scilabコード

Scilabコードは以下になる。
x = [0.51, 0.76, 1.06, 1.41, 1.75, 1.9, 2.01, 2.15, 2.27, 2.4, 2.49, 2.59, 2.67, 2.76, 2.83, 2.89, 2.95, 3.01, 3.05, 3.11, 3.15, 3.19, 3.23, 3.28, 3.31, 3.34, 3.38, 3.4, 3.43, 3.46, 3.49, 3.51]';
y = [10, 11, 12, 13, 14, 14.5, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40]';
A=[x,ones(x)];B=y; // 各項と結果
coef=lsq(A,B); // 最小二乗法で得られた1次関数の各係数
disp('各係数');
disp(coef);
plot(x,y,'+')
xp=linspace(0,4,400); // x軸
fx=coef(1)*xp+coef(2); // 2次関数
plot(xp,fx,'-k')
p=gca();p.tight_limits(:)="on";
p.data_bounds(:,2)=[10;41];
p.data_bounds(:,1)=[0;4];実行結果

結果は以下になる。
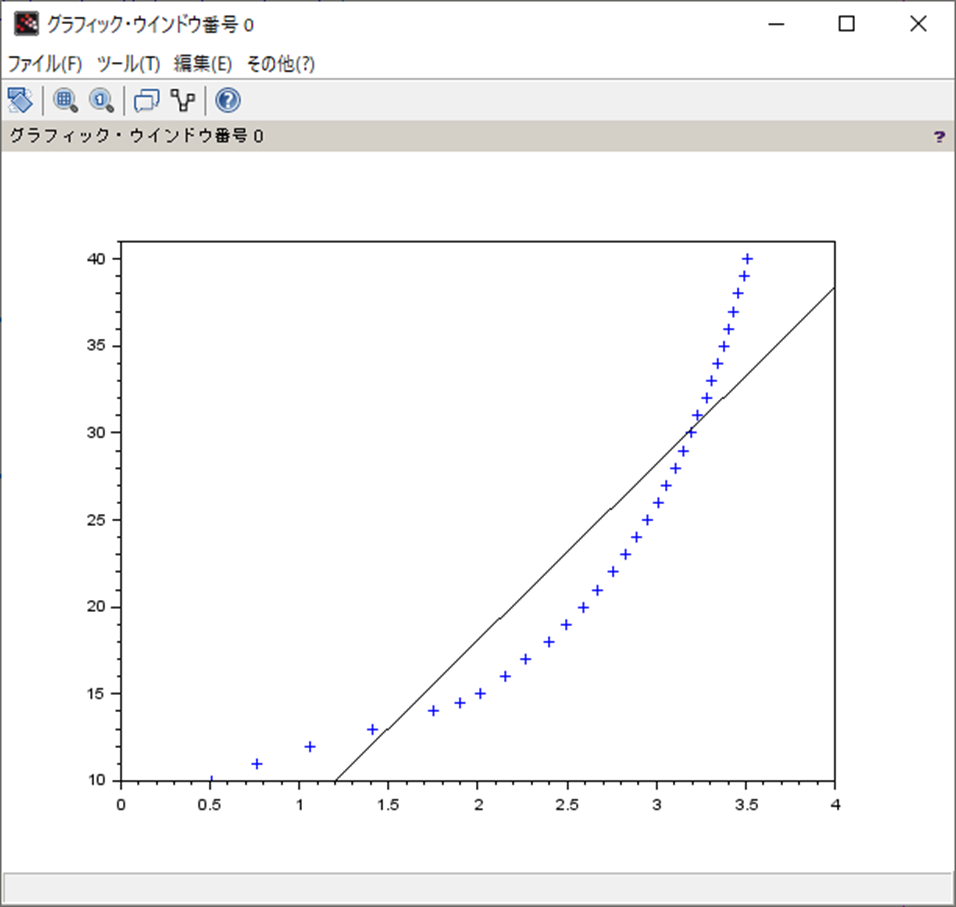
各係数
10.133034
- 2.1616644 
これも係数の値が微妙に違うけど、表示精度の問題を加味すると同じ値と見なせるのかな?

うん。同値と見なしてOKだろう。

以下がScilabによる係数算出のところだよね。
A=[x,ones(x)];B=y; // 各項と結果
coef=lsq(A,B); // 最小二乗法で得られた1次関数の各係数
そうそう。
Aに各項を入れる。
\(x^2\)のように二次の項を入れていけば、polyfitのような多項式に対する最小二乗法が実現できるし、
\(x\)以外の変数を入れると重回帰分析になる。
まぁ、正規方程式のルールを適用できるってことだな。

意味わからん。

正規方程式については追々説明する予定だから、そういうものがあるって程度の認識で良いよ。

了解!
まとめ

まとめだよ。
- Scilabによる1次関数の最小二乗法を実施。
- MATLABと一緒と思いきや、実はコンセプトレベルで違う。
- 正規方程式の仕様が丸見えになってるイメージ。
- 正規方程式については追々説明していく予定。
バックナンバーはこちら。




コメント