バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
まずは最もシンプルな回帰分析である、
1次関数の最小二乗法についての説明の続き。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
誤差関数の最小値を求めるには?(2回目)

前回は、誤差関数の最小値を総当たりで求める話のあとに、
偏微分がどうのこうのってなったけど?

うん。
まずは誤差関数を再掲しておこう。
\(
\begin{eqnarray}
L(a,b)&=&\displaystyle\sum_{i=0}^n\{y_i -(ax_i +b)\}^2 \\
&=&\displaystyle a^2\sum x_i^2+nb^2+\sum y_i^2-2a\sum x_i y_i -2b\sum y_i +2ab\sum x_i
\end{eqnarray}
\)

そして、\(a\)に於いての偏微分が0、\(b\)に於いての偏微分が0の部分が最小二乗法で欲しい\(a,b\)の条件となる。
式にするとこんな感じ。
\(
\displaystyle \frac{\partial L(a,b)}{\partial a}=0,\frac{\partial L(a,b)}{\partial b}=0
\)

出来てきたー偏微分ーーー!!

まぁ偏微分ではあるけど、ここでは普通の微分と捉えてOKだ。

普通の微分でもアウトなんだが・・・。
この偏微分は何を示している?

で、この偏微分は一体何を示しているの?

前回の\(a\)と\(b\)を総当たりで値を振ったときを思い出してほしいのだけど、
両方とも、2次関数的な軌跡を描いていたよね?

確かに2次関数的だった。

というわけで、その双方が最小値になった時がもっとも誤差が小さいときと言える。
図で説明するとこんな感じだな。
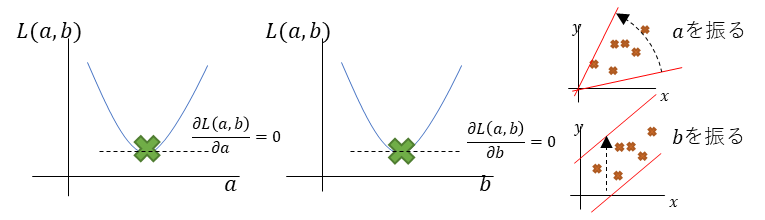

そっか。
微分の性質として、0になる点は極大値か、極小値になって、
最小二乗法に於いては必ず極小値になるってことなのか。
だから、偏微分して0が誤差が最も少ない点。
ってことになるんだな。

そうそう。
偏微分をどう解くのか

いや、ちょっと待って。
偏微分で誤差関数の最小値が求められるというのは理解できたけど、
そもそも具体的な値として求められるものなの?
なんか全然イメージ沸かない。

誤差関数自体はすでに求まっているので、
それに対して偏導関数を導出するだけだな。

で、その偏導関数の導出って・・・。

そこも含めて次回解説だな。

よろしく頼むーー!
まとめ

まとめだよ。
- 誤差関数の最小値は偏微分を使用すると求まるはず。
- a,bを振ったい場合の誤差関数の値は2次関数的になるので、極値は必ず極小値になる。
- この極小値になるa,bを求めたい。
バックナンバーはこちら。




コメント