バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
まずは最もシンプルな回帰分析である、
1次関数の最小二乗法についての説明をする。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
1次関数の最小二乗法

まずは1次関数の最小二乗法から説明していこう。
これはもっともシンプルな回帰分析と言える。

最小二乗法は、名前は知ってるけど、
具体的に何してるとかはわからないんだよなー。

前回の、複数のプロットを元に最もそれらしい線を引く。
ってのを実現しているものだな。

その「最もそれらしい線」っていうのをどう特定しているのか?
ってところがわからん。
最もそれらしい線の特定方法

「最もそれらしい線」の特定方法は、
各サンプリングとの誤差が最小となる線だな。
以下のイメージだ。
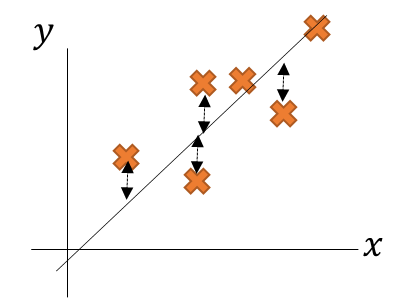

まぁ、言いたいことはわかる。

そして、「誤差が最小」という部分だが、
単純に引き算で求めると、サンプリングと線の位置関係が上か下かで符号が逆転してしまう。
それを抑制するために「誤差の二乗の和が最小になる線」を特定することになる。

そっか。
二乗にすれば、符号の問題は無くなるもんね。
それに、こういうことをするから最小二乗法って名前なのか。

そうそう。
誤差関数

そして、「誤差の二乗の和が最小になる線」を求める際に最小を目指すための関数を誤差関数と呼ぶのだけど、
1次関数の最小二乗法にとっての誤差関数を特定する必要がある。

どう特定するの?

まず、以下が誤差が最小の関数であると仮定する。
\(ax+b=y\)

普通の一次関数だね。

サンプリングした\((x,y)\)を元に\((a,b)\)を求めたいので、
最小化したい誤差関数\(L\)を求める。
\(
\begin{eqnarray}
L(a,b)&=&\displaystyle\sum_{i=0}^n\{y_i -(ax_i +b)\}^2 \\
&=&\displaystyle a^2\sum x_i^2+nb^2+\sum y_i^2-2a\sum x_i y_i -2b\sum y_i +2ab\sum x_i
\end{eqnarray}
\)

なんかややこしいことになっているような・・・。

一見するとややこしいかもしれないが、
これが最終的にはシンプルになる。

そうなの?

あと、このシリーズってベクトルとか、行列をいい感じに使って
計算を楽にしようとしてると思ったのだけど、
今のところ、ベクトルも行列も出てきてないね。

それもすぐ出てくる。
まぁ行列で表現するが故にシンプルになるんだけど。

まぁ、そこは期待して聞いておこう。
nb^2について

さっきの誤差関数の中に\(nb^2\)ってのがいたけど、
そんなのが出るような式だったっけ?

あー、あれは以下の変形をした結果だな。
\(
b^2\sum 1=nb^2
\)

なぜ、これがイコールで結ばれるのかがわからん・・・。

\(\sum 1\)って丁寧に書くと以下になる。
\(\displaystyle\sum_{i=1}^5=1+1+1+1+1=5\)

あ、そっか。
n個の1の和だから、nになるのか。

そうそう。
まとめ

まとめだよ。
- 最もシンプルな回帰分析である1次関数の最小二乗法の解説開始。
- 最小二乗法の理屈は「誤差の二乗の和が最小になる線」を求める。
- 誤差が最小になる関数を誤差関数Lとして定義。
- 1次関数に於いて最小になる誤差関数を求めた。
- 後々、シンプルな式になる予定。
バックナンバーはこちら。




コメント