バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia2-backnumber/
はじめに
第2章がこれから始まる。
内容としては最小二乗法を始めとした回帰アルゴリズムがメインのシリーズとなる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
これから何をするのか

こらから第2章が始まるわけだけど、
具体的には何をやる予定なの?

最小二乗法を代表とした回帰アルゴリズムをメインにやる予定。

回帰?

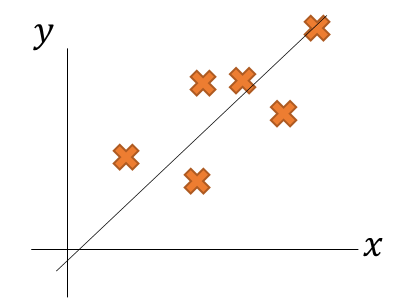
以下みたいな感じで
プロットされた点に対して、
もっともらしい線を引くようなものを回帰分析と呼ぶ。
回帰(、英: regression)とは、統計学において、Y が連続値の時にデータに Y = f(X) というモデル(「定量的な関係の構造」)を当てはめること。別の言い方では、連続尺度の従属変数(目的変数)Y と独立変数(説明変数)X の間にモデルを当てはめること。X が1次元ならば単回帰、X が2次元以上ならば重回帰と言う。Y が離散の場合は分類と言う。
Wikipediaより(https://ja.wikipedia.org/wiki/%E5%9B%9E%E5%B8%B0%E5%88%86%E6%9E%90)

あー、こういうは見たことあるな。
どういうふうに役立つのか?

んで、この回帰が出来ると何がうれしいんだ?

まぁサンプリングしたデータの特性が分かりやすくなるというのが多いだろうが、
自動車業界だと、制御対象の内部パラメータの推定で使われることもあるな。

推定?
そんなことができるの?
最小二乗法での推定例

例えば、モータあったとして、
そのモデルと以下とする。
\(
I(t)=\displaystyle \frac{E(t)}{R}+b
\)

実際は逆起電力が入るからこんなシンプルにはならないんだけど、
あくまで例としてシンプルな式にしている。

電圧と電流の関係を表してる式ってことだよね。

で、ここの抵抗値\(R\)とバイアス\(b\)は
本来は定数で、変化しない前提で計算されることが多いのだけど、
現実世界ではそういうわけにはいかない。
例えば、経年劣化で定数が変わって特性が変わってしまうことがあり得るからだ。

あー、たしかに経年劣化は最大の敵に一つだなぁ。

ここで、電圧に対して電流が計測できるとすると以下のようにプロットができる。
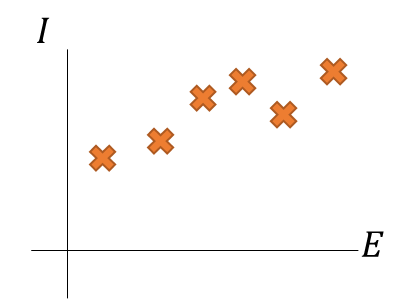

入力が電圧で出力が電流って位置づけだね。

そこに先ほどのモデルと同じように1次式として、
それっぽい線を引くと以下になる。
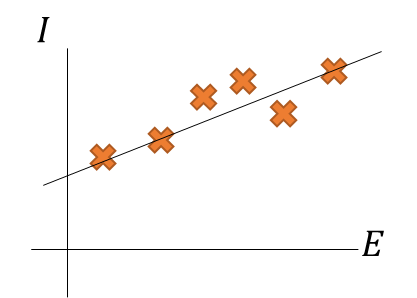

まぁ妥当そうな線だ。

この一次式が以下とすると・・・。
\(
I(t)=0.5 E(t)+2
\)

先ほどのモータモデルの数式に当てはめると・・・。
\(
\begin{eqnarray}
1/R&=&0.5 \\
R&=&2 \\
b&=&2
\end{eqnarray}
\)

あ、不明だった定数が求まった!

これが回帰アルゴリズムを利用したパラメータ推定の例だな。
これにより経年劣化後のパラメータも適時推定できるので、
- 故障前に劣化状況を検知
- 劣化状況に合わせた制御ポリシーに変更
なんてことが可能になる。

確かにこれは便利そうだ。
まとめ

まとめだよ。
- 本シリーズは最小二乗法を代表とした回帰アルゴリズムメイン
- 自動車業界だと、制御対象の内部パラメータの推定で使われることもある。
- 経年劣化で内部パラメータが変動しても回帰である程度特定可能。
- これにより事前交渉検知や劣化状況に合わせた制御ポリシーの変更が可能。
- 経年劣化で内部パラメータが変動しても回帰である程度特定可能。
バックナンバーはこちら。




コメント