バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回は、PID制御の数式をオイラー法で微分解決して離散化した。
数式上はカオスに見えるが、似たような式が並んではいる。
これがブロック線図にする際にいい感じに効いてくる。(はず)
というわけで、今回はブロック線図を起こす。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
前回のPID制御の離散化

前回は・・・PID制御の離散化をしたが、
数式的にはとんでもないことになったな・・・。

一応、必要な式を再掲しておこう。
\(
\displaystyle\int x(t)dt=\sum x(t-\Delta T)+x(t)\frac{\Delta T}{T_1}
\)
\(
\eqalign{
u(t)&=&\int\{K_p \dot{e}(t) + K_i e(t)dt + K_d \ddot{e}(t)\}dt\cr
&=&\int\{\color{red}{\{K_p\frac{T_1}{\Delta T}\{e(t)-e(t-\Delta T)\}}\color{black}+K_ie(t)\cr
&+&K_d\frac{T_1}{\Delta T}\{\color{blue}{\{\frac{T_1}{\Delta T}\{e(t)-e(t-\Delta T)\}}\cr
&-&\color{blue}{\frac{T_1}{\Delta T}\{e(t-\Delta T)-e(t-2\Delta T)\}}\color{black}\}\}dt
}
\)

一応、色分けした部分があって、その部分は共通化はできるようだけど、
カオスさが減るイメージはないんだよな。

まぁここは実際にブロック線図を見てから、再度感想を聞こうか。
ブロック線図

そして、上記数式に合わせて起こしたブロック線図が以下。
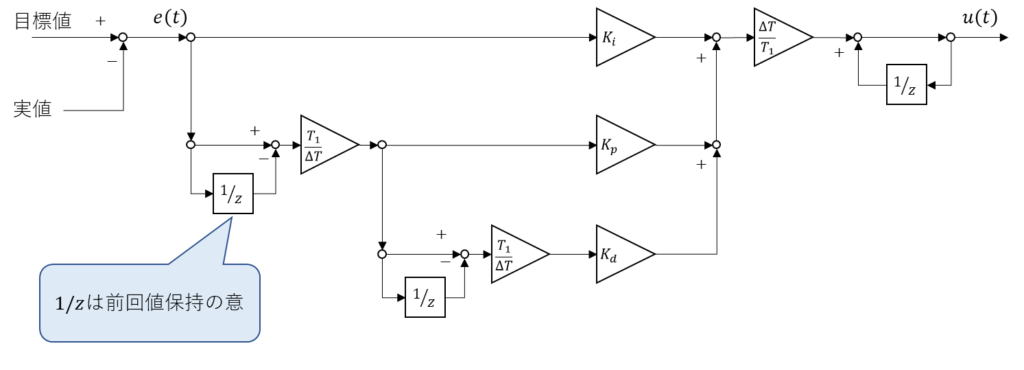

あれ?!
思ったよりもあっさりになったぞ!

そうか。
同じ数式のところはブロック線図としては同一の信号線を参照すれば良いからいい感じに最適化されるのか。

そうそう。
これで処理のイメージは湧きやすくなったと思う。
PID制御器を加味した構成図

そしてPID制御器を加味した構成図が以下となる。
ちなみに、PID制御器内部はおおよそ-1~1の範囲で値が動くよう
フィードバック側は1/60にしている。
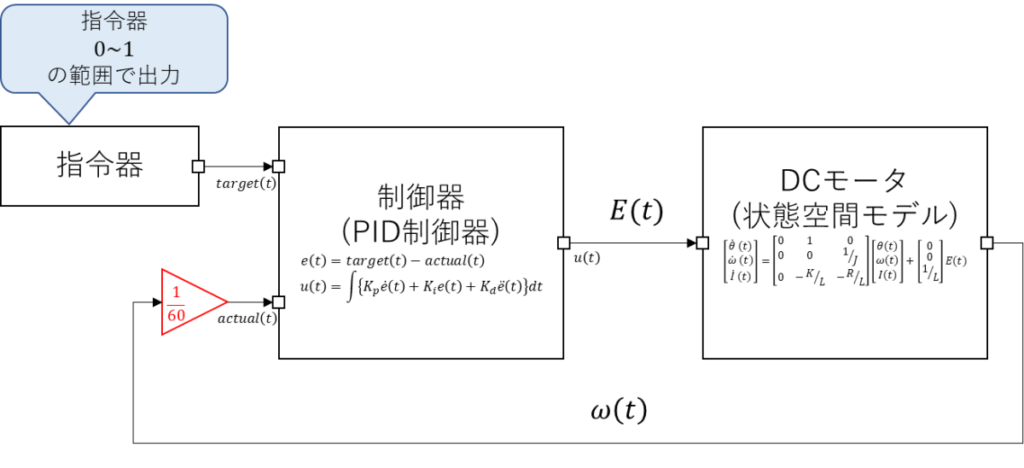

1/60?
どこから来た数値?

\(E(t)=1\)とした際に、角速度\(\omega(t)\)はおおよそ\(60[rad/sec]\)に収束してたんだよね。
PID制御器の内部信号の動作範囲を-1~1としたい場合は1/60するとちょうど良い感じになるはずだ。

なるほど。
いわゆる正規化ってやつだね。

そうそう。
こうすることでPID制御器は割と純粋な数学の世界で動作するから挙動が読みやすくなる。
そして次は

じゃー、これでPID制御は完了!

いや?まだだよ?

わかってるよー。
シミュレーションするんでしょー?

そうそう。
ブロック線図からコードに落とし込んで、
以前作成したDCモータの状態空間モデルと接続する感じだな。

そう考えると結構めんどそうだな。

構成図、ブロック線図、ソースコードの3点セットで見ればわかりやすいかもね。

じゃー次回からそんな感じでコードを起こしていく回になるわけか。
まとめ

まとめだよ。
- PID制御離散化式からブロック線図を作成。
- 同一の数式が埋まっている箇所は同一の信号線を参照できる。
- よって、比較的にシンプルになる。
- 同一の数式が埋まっている箇所は同一の信号線を参照できる。
- 正しさの証明はやはりシミュレーション。
- 構成図、ブロック線図、ソースコードの3点セットで見て行けばそれほど混乱はしない。(たぶん)
バックナンバーはこちら。




コメント