バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回は、状態空間モデルの数式の各要素について説明。
- 状態方程式と出力方程式。
- 状態量、入力量、出力量
- 状態行列、入力行列、出力行列、直達行列。
説明はしたが、使い方が分かり難いというのが論点ということも認識はしている。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
状態空間モデルの使い方を知るためには?

前回は、状態空間モデルの各要素の説明はしてもらったけど、
やっぱりわからん。

具体的に何がわからんの?

結局のところは使い方かなぁ?
まぁ使ってる状況を見ても良く分からんから、もうどうしたら良いか・・・。

ふむ。
ならば、超シンプルな状態空間モデルを一度作ってみるか。

超シンプル?

普通は複数の微分方程式を内包するのが状態空間モデルの醍醐味なのだけど、
そこは一旦目をつむって使い所は無いかもしれないけど、シンプルな微分方程式を扱ってみる。
って感じ。

なるほど。
そういうのをやってもらえると理解できるかも。
シンプルな微分方程式

で、そのシンプルな微分方程式な何にするの?

物理現象でシンプルな微分方程式といったらもう
「ニュートンの運動方程式」だな。

あー、こんなやつか。
ニュートンの運動方程式
\(\vec{F}=m\vec{a}\)

そう。それそれ。
そして、入力と出力に関しては
入力は力\(\vec{F}\)、出力は距離\(\vec{s}\)と速度\(\vec{v}\)としよう。
絵にするとこんな感じだな。
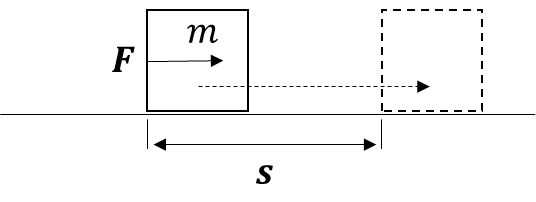

真面目に問いを出すと以下の感じかな。
質量\(m\)の物体を、力\(\boldsymbol F\)を加え続けて距離\(\boldsymbol s\)分移動させた。
距離\(\boldsymbol s\)を出力(観測)とした状態空間モデルを作成せよ。
尚、運動方程式は以下とし、摩擦や重力は無視する。
\(m \ddot{s}(t)=\boldsymbol F(t)\)

なんか数学の問題文みたいなことに・・・。

一見何言ってるかわからんかもしれんけど、
一個ずつ紐解けばそれほど複雑話では無い。

まぁ扱ってる式、変数、係数は最小の部類だろうから、まずはこれで理解していくしかないのか・・・。
まとめ

まとめだよ。
- 状態空間モデルの各要素は分かれど使い方はわからない。
- 使い方を見てもよくわからない。
- よって、超シンプルな微分方程式を対象に状態空間モデルを作ってみる。
- ニュートンの運動方程式を対象とする。
バックナンバーはこちら。




コメント