プログラム化に向けて
だいたい理屈の部分はやった感じなので、
これからプログラム化に向けての話になる。
今回も処理のフローを書いておこう。
と言っても、前回の逆伝播のフローとおおよそ一緒。
- データセットの定義
- ハイパーパラメータの設定
- 学習率
- エポック数
- パラメータの初期値、
- シグモイド関数の導関数の定義
- 順伝播
- 誤差計測
- 逆伝播
- バイアスの逆伝播
- 重みの逆伝播
- パラメータの更新
- 重みの変化の経緯をplot
例によって、順伝播、逆伝播、パラメータの更新で1セットで何回もループする。
これは前回の逆伝播と一緒。
差分はパラメータの初期値がランダムになったこととと、
バイアスも加味して学習するという点。
どんな感じに動くのか
さて、プログラムとして実現できそうってことはわかったが、
結局どんな感じの学習になるのかがイメージが沸きにくい。
よって、ここは決定境界線の位置を学習回数(エポック)が進むとどうなるかを見てみよう。
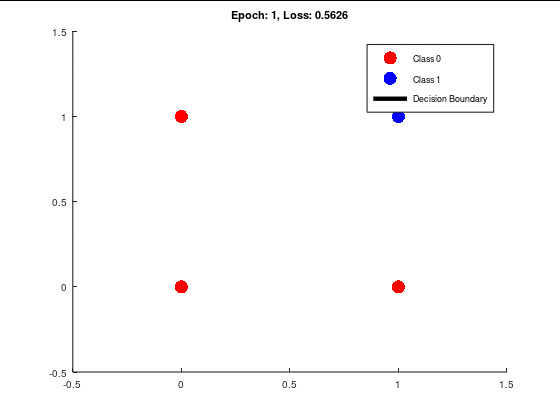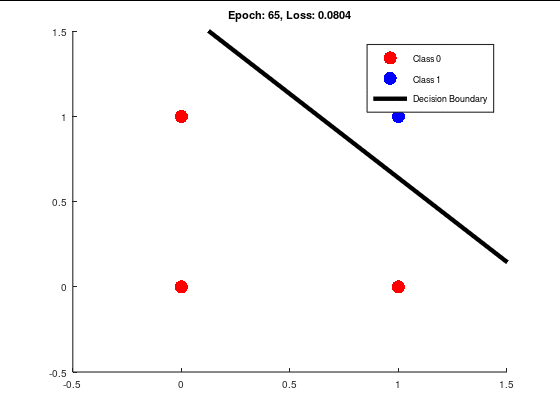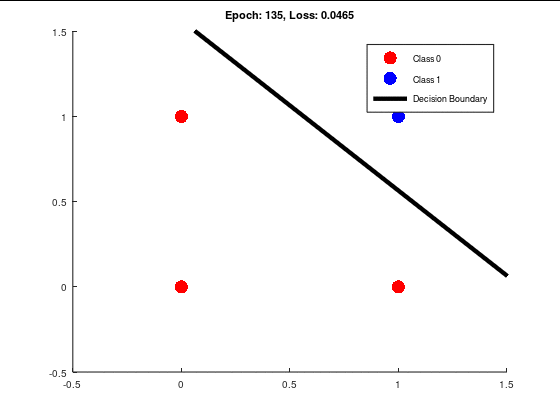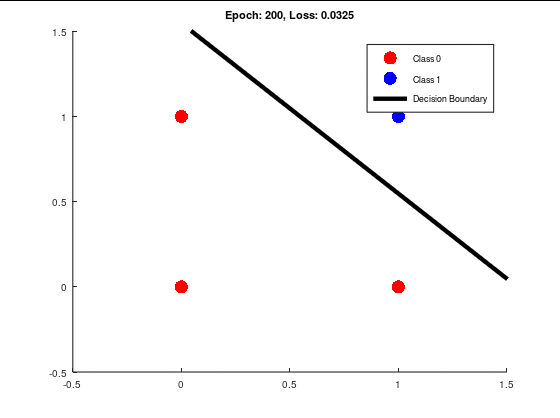
こんな感じで、経緯が見れるようにしておくと面白いかもしれない。
ただし、今回作成するプログラムでは特にアニメーションはさせない。
まとめ
- 単純パーセプトロンの構造について復習。
- 逆伝播の復習。
- 重みとバイアスの連鎖律の最適化。
- 単純パーセプトロンで分類のプログラムのフローを確認。
- 学習が進むと決定境界線がどのように動くか確認。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ！あたらしい線形代数の教科書
Amazon.co.jp: Pythonで動かして学ぶ！あたらしい線形代数の教科書 eBook : かくあき: Kindleストア
Amazon.co.jp: Pythonで動かして学ぶ！あたらしい線形代数の教科書 eBook : かくあき: Kindleストア
amzn.to
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装 | 斎藤 康毅 |本 | 通販 | Amazon
Amazonで斎藤 康毅のゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装。アマゾンならポイント還元本が多数。斎藤 康毅作品ほか、お急ぎ便対象商品は当日お届けも可能。またゼロから作るDeep Lea...
amzn.to
ゼロからはじめるPID制御
ゼロからはじめるPID制御 | 熊谷 英樹 |本 | 通販 | Amazon
Amazonで熊谷 英樹のゼロからはじめるPID制御。アマゾンならポイント還元本が多数。熊谷 英樹作品ほか、お急ぎ便対象商品は当日お届けも可能。またゼロからはじめるPID制御もアマゾン配送商品なら通常配送無料。
amzn.to
OpenCVによる画像処理入門
OpenCVによる画像処理入門 改訂第3版 (KS情報科学専門書) | 小枝 正直, 上田 悦子, 中村 恭之 |本 | 通販 | Amazon
Amazonで小枝 正直, 上田 悦子, 中村 恭之のOpenCVによる画像処理入門 改訂第3版 (KS情報科学専門書)。アマゾンならポイント還元本が多数。小枝 正直, 上田 悦子, 中村 恭之作品ほか、お急ぎ便対象商品は当日お届けも可能。...
amzn.to
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門] | 金城俊哉 | 数学 | Kindleストア | Amazon
Amazonで金城俊哉の恋する統計学 恋する統計学。アマゾンならポイント還元本が多数。一度購入いただいた電子書籍は、KindleおよびFire端末、スマートフォンやタブレットなど、様々な端末でもお楽しみいただけます。
amzn.to
Pythonによる制御工学入門
Amazon.co.jp
amzn.to
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析
Amazon.co.jp
amzn.to
コメント