MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その69【単純パーセプトロンで分類⑤】
を書き直したもの。
単純パーセプトロンで分類を行う。
今回はPythonで実現。
単純パーセプトロンで分類のプログラムのフロー【再掲】
単純パーセプトロンで分類するプログラムのフローを再掲。
- データセットの定義
- ハイパーパラメータの設定
- 学習率
- エポック数
- パラメータの初期値、
- シグモイド関数の導関数の定義
- 順伝播
- 誤差計測
- 逆伝播
- バイアスの逆伝播
- 重みの逆伝播
- パラメータの更新
- 重みの変化の経緯をplot
重みとバイアスへの連鎖律への共通式
\(
\begin{eqnarray}
\displaystyle dZ&=&\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}=(A-Y)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot X\\
&=&
\Bigg(
\begin{bmatrix}
a_1\\a_2\\a_3\\a_4
\end{bmatrix}-
\begin{bmatrix}
0\\0\\0\\1
\end{bmatrix}
\Bigg)\circ
\sigma\Bigg(
\begin{bmatrix}
z_1\\z_2\\z_3\\z_4
\end{bmatrix}
\Bigg\{
1-\sigma\Bigg(
\begin{bmatrix}
z_1\\z_2\\z_3\\z_4
\end{bmatrix}
\Bigg)
\Bigg\}
\end{eqnarray}
\)
重みへの連鎖律
\(
\displaystyle\frac{\partial E}{\partial W}=dZ^TX=
\begin{bmatrix}
dz_1\\dz_2\\dz_3\\dz_4
\end{bmatrix}^T
\begin{bmatrix}
0&0\\
0&1\\
1&0\\
1&1\\
\end{bmatrix}
\)
バイアスの連鎖律
\(
\displaystyle\frac{\partial E}{\partial b}=\sum dZ=
\begin{bmatrix}
dz_1\\dz_2\\dz_3\\dz_4
\end{bmatrix}^T
\begin{bmatrix}
1\\1\\1\\1
\end{bmatrix}
\)
これをPythonで実現する。
Pythonコード
Pythonコードは以下。
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoid_derivative(x):
return sigmoid(x) * (1 - sigmoid(x))
# データセットの定義
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([[0], [0], [0], [1]])
# ハイパーパラメータの設定
learning_rate = 0.5
num_epochs = 200
# パラメータの初期化
W = np.random.randn(1, X.shape[1])
b = np.random.randn()
for epoch in range(1, num_epochs + 1):
# 順伝播
Z = X@W.T + b
A = sigmoid(Z)
# 誤差計算
loss = np.mean((A - Y) ** 2)
# 逆伝播
dZ = (A - Y) * sigmoid_derivative(Z)
dW = dZ.T@X
db = np.sum(dZ)
# パラメータの更新
W = W - learning_rate * dW
b = b - learning_rate * db
print(f'W={W}')
print(f'b={b}')
# プロット
plt.scatter(X[Y.flatten() == 0, 0], X[Y.flatten() == 0, 1], c='r', marker='o', label='Class 0')
plt.scatter(X[Y.flatten() == 1, 0], X[Y.flatten() == 1, 1], c='b', marker='o', label='Class 1')
x1 = np.array([np.min(X[:, 0]) - 1, np.max(X[:, 0]) + 1])
x2 = -(W[0, 0] * x1 + b) / W[0, 1]
plt.plot(x1, x2, 'k', linewidth=2)
plt.xlim([-0.5, 1.5])
plt.ylim([-0.5, 1.5])
plt.title(f'Epoch: {epoch}, Loss: {loss:.4f}')
plt.legend(loc='upper right')
plt.xlabel('X1')
plt.ylabel('X2')
plt.grid()
plt.show()処理結果
処理結果は以下。
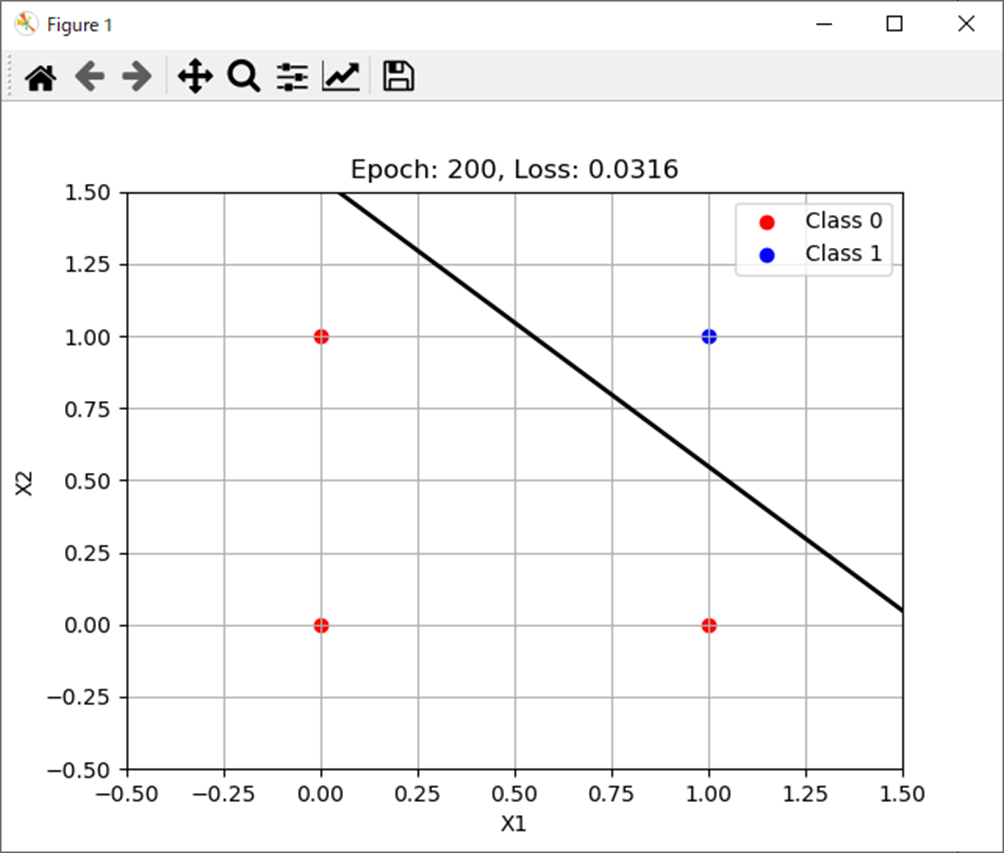
W=[[2.65017116 2.65730987]]
b=-4.105401923669778まとめ
- 単純パーセプトロンの分類をPythonで実施。
- 想定通り分類可能。
- おおよそ200エポックあれば分類可能。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析





コメント