MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その40【多変量関数の連鎖律④】
MATLAB,Python,Scilab,Julia比較 第4章 その41【多変量関数の連鎖律⑤】
MATLAB,Python,Scilab,Julia比較 第4章 その42【多変量関数の連鎖律⑥】
を書き直したもの。
多変量関数の連鎖律の解説。
今回は以下の話。
- 多変数関数の連鎖律
- ニューラルネットワークを意識した場合
- 学習データの多入力による暗黙的関数追加
【再掲】多変量関数の連鎖律を把握するための知識
とりあえず多変量関数の連鎖律を把握するための知識を再掲。
- 合成関数(済)
- 合成関数の微分(連鎖律)(済)
- 多変数関数の連鎖律
- 学習データの多入力による暗黙的関数追加
多変数関数の連鎖律とは?
前回、合成関数の微分(連鎖律)をやったので、
それの多変量化の話になる。
やることは一緒。
ただし数が増える。
であるが故に微分が偏微分になる。
偏微分は変な微分なイメージが強いかもしれないが、
複雑なものを簡単に解釈できるツールだと思ってもらった方が良い。
(複雑なものを簡単に解釈できるが故に複雑なシーンで利用されてるだけで・・・。)
とりあえず、ここでは普通の微分のつもりで見ておけばOK。
多変量と言っても、まずは2入力で考える。
実際、今回使用する単純パーセプトロンの入力も2つなので。
多変数関数の連鎖律
まずは、該当関数の構成を図示しよう。
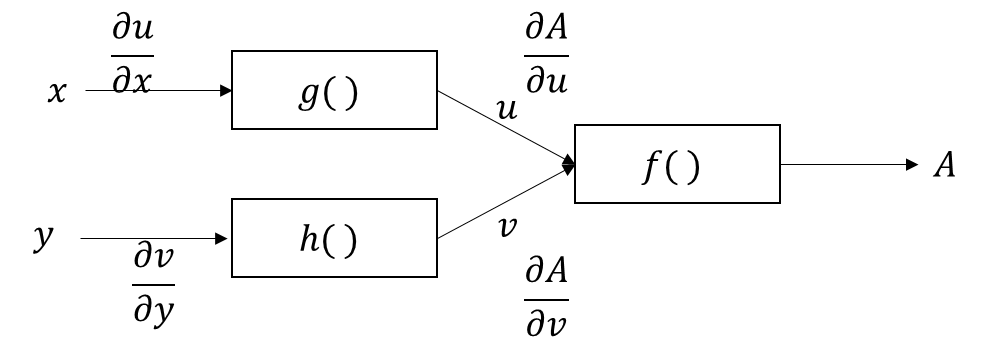
\(x,y\)が入力で、\(g(),h()\)をて\(u,v\)となる、
\(f(u,v)\)を経て\(A\)になる。
って関数になる。
各所の偏微分がはっきりしていればあとは簡単。
連鎖律の理屈で繋げるだけ。
以下の数式になる。
\(
\begin{eqnarray}
\displaystyle \frac{A}{x}=\frac{A}{u}\frac{u}{x}\\
\displaystyle \frac{A}{y}=\frac{A}{v}\frac{v}{y}\\
\end{eqnarray}
\)
図と数式をセットにしてあると、
そんなもんかって程度になると思う。
というわけで、多変量になっても数が増えるだけってことだ。
ニューラルネットワークを想定した場合はもう少し複雑になるが。
ニューラルネットワーク的な感じで関数構成を書き直す
多変量関数の連鎖律をニューラルネットワークで想定した場合に少し厄介になる。
まずは、想定関数構成を見せよう。
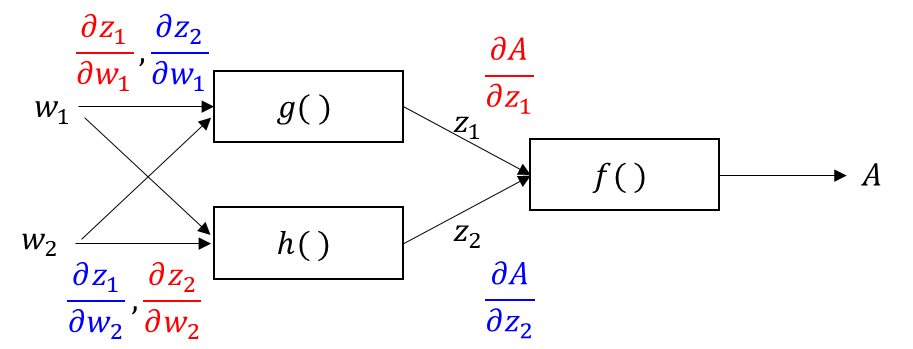
先ほどの図に似ているが、入力がそれぞれの関数に入ってる感じが違う点。
よって、連鎖律の経路が少し複雑になる。
加えて、ニューラルネットワークの場合、動かしたい値は入力ではなく、重みの方。
よって、重みが連鎖律に於ける入力になる。
と言っても基本的な考え方は変わらない。
ニューラルネットワーク的な感じで関数構成の連鎖律を数式で
先ほどの関数構成を元に連鎖律を書き出すと以下になる。
\(
\begin{eqnarray}
\displaystyle \frac{A}{w_1}=\frac{A}{z_1}\frac{z_1}{w_1}+\frac{A}{z_2}\frac{z_2}{w_1}\\
\displaystyle \frac{A}{w_2}=\frac{A}{z_1}\frac{z_1}{w_2}+\frac{A}{z_2}\frac{z_2}{w_2}\\
\end{eqnarray}
\)
\(w_1,w_2\)ともに\(z_1,z_2\)の経路を通るので、
それぞれの経路の連鎖律を合成すればOK。
「合成すればOK」な理由は、
それぞれの変化が求まるから、変化の合計がトータルの変化だから。
これがニューラルネットワークを想定した場合の多変量関数の連鎖律になる。
次のページへ
次のページでは、「学習データの多入力による暗黙的関数追加」の話





コメント