【入門】多変量関数の連鎖律①【数値計算】

はじめに

の、

MATLAB,Python,Scilab,Julia比較第4章その37【多変量関数の連鎖律①】
MATLAB,Python,Scilab,Julia比較第4章その38【多変量関数の連鎖律②】
MATLAB,Python,Scilab,Julia比較第4章その39【多変量関数の連鎖律③】

を書き直したもの。

連鎖律を把握するための解説。
今回は多変量じゃない合成関数(連鎖律)、それの微分、それの証明の話になる。

まずは、連鎖律を把握するための知識を再掲

今回は、多変量関数の連鎖律に突入・・・。
なのだが、これは割とボリュームがある。

「多変量関数の連鎖律」に必要な知識を分解すると以下になる。

これらを各個撃破していく。

まずは合成関数。
これは名前の通り、合成した関数。
図示するとこれになる。

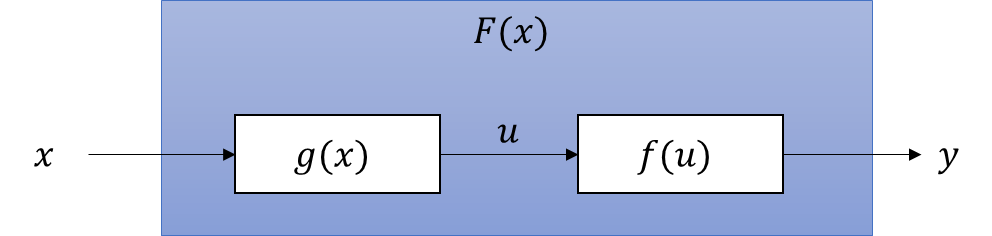
そして、これを数式で示したのがこれ。

\(
\begin{eqnarray}
y&=&f(x)\\
y&=&f(g(x))\\
F(x)&=&f(g(x))
\end{eqnarray}
\)

というわけで、関数の入力に関数を入れ込む感じのものになる。

この例では2つの関数を合成しているが、
これが3つ、4つになってもOK。
そして、単純パーセプトロンは入力層の内積、活性化関数、誤差関数がそれぞれ関数と見なせる。
つまり、合成関数で表現可能。

実際は多変量な入力を受け付けるので、これだけでは表現できないが、
ここで重要なのは関数がネストしていることと一緒という点を認識できればOK。

合成関数の微分の話になるが、
これがいわゆる連鎖律と言うものになる。
今の段階ではまだ多変量の話にはなっていないが、まずは1入力1出力な関数でイメージを固めた方が良い。
そのあとに多変量で考え直す。
その後に勾配降下法。
という流れを想定。

まず今回、合成関数の微分を行いたい関数の構成を図示する。

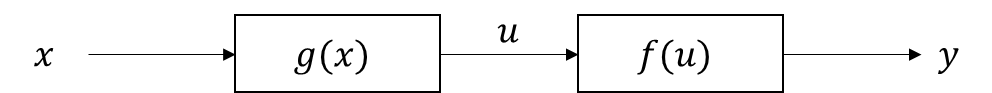
数式にすると以下になる。

\(
\begin{eqnarray}
y&=&f(u)\\
u&=&g(x)\\
y&=&f(g(x))\\
\end{eqnarray}
\)

先ほどの関数の構成で合成関数の微分をすると以下が成立する。

\(
\displaystyle\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}
\)

ここで「なんで？」と思ったと思うが、
本当にこうなる。
一応証明可能だが、まぁまぁカオス。
合成関数の微分をテクニックとしてそのまま飲み込むパターンでも良い気はするが、
一応証明もしてみる。

次のページで合成関数の証明をする。