MATLAB、Python、Scilab、Juia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
MATLAB,Python,Scilab,Julia比較に於ける、
以下を元に書き直したもの。
- MATLAB,Python,Scilab,Julia比較 その23【行列演算⑥】
- MATLAB,Python,Scilab,Julia比較 その24【行列演算⑦】
- MATLAB,Python,Scilab,Julia比較 その25【行列演算⑧】
- MATLAB,Python,Scilab,Julia比較 その26【行列演算⑨】
- MATLAB,Python,Scilab,Julia比較 その27【行列演算⑩】
- MATLAB,Python,Scilab,Julia比較 その28【行列演算⑪】
- MATLAB,Python,Scilab,Julia比較 その29【行列演算⑫】
- MATLAB,Python,Scilab,Julia比較 その30【行列演算⑬】
線形代数の基礎について記載していく。
説明の流れ
以下の流れで説明して行く。
- 行列の内積の公式の再確認
- 方程式と内積
- 連立方程式と行列
- 行列によるベクトル変換
- 行列によるベクトル群変換
「方程式と内積」については、
余弦定理についての証明も含めている。
行列の内積の公式の再確認
以下が2×2行列の内積の公式となる。
\(
\begin{bmatrix}
a & b \\
c & d
\end{bmatrix}
\begin{bmatrix}
e & f \\
g & h
\end{bmatrix}=
\begin{bmatrix}
ae+bg & af+bh \\
ce+dg & cf+dh
\end{bmatrix}
\)
なぜ、このような公式になるのかを知ることが本記事の目的となる。
内積の定義
内積の定義は以下となる。
\(
\vec A \cdot \vec B = |A||B|\cos(\theta)
\)
演算子は省略されることもあるが、
基本的には”\(\cdot\)”になる。
このことからドット積とも呼ばれる。
そして、計算結果がベクトルからスカラーになることから
スカラー積とも呼ばれる。
内積自体は特に意味はなく、そういう計算という意味しかない。
ただし、特性のようなものはある。
内積の特性
内積の特性は、2つのベクトルの相関性を知ることができるというもの。
\(|a||b|\cos(\theta)\)を図示すると以下になる。
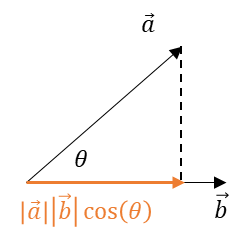
そして、\(\vec b\)のノルム(大きさ)が1とした場合、
内積の結果が1に近いほど\(\vec a\)と\(\vec b\)は似ている。
ということになる。
考え方は類似度と呼ばれてて、
特に今回のやり方はcos類似度って呼ばれてる
それ以外の特性としては以下。
- 畳み込み積分(合成積)そのもの。
- 類似成分の抽出。
- 方程式と強い関係性あり。
様々な数学的テクニックの基本となっており、
そのため、内積を問うということは掛け算割り算を問うことと一緒であり、意味を持たない。
余弦定理
内積と方程式を紐づけるには余弦定理が必要。
余弦定理(よげんていり、英: law of cosines, cosine formula)とは、平面上の三角法において三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理である。余弦定理を証明するために用いられる補題はときに第一余弦定理と呼ばれ、このとき証明される定理は第二余弦定理と呼ばれ区別されることがある。単に余弦定理と言った場合、第二定理を指す。
Wikipediaより(https://ja.wikipedia.org/wiki/%E4%BD%99%E5%BC%A6%E5%AE%9A%E7%90%86)
Wikipediaにある通り、今回言ってる余弦定理は第二余弦定理の方で、
第二余弦定理は以下になる。
\(a^2=b^2+c^2-2bc\cos(\alpha)\)
ここで出てくる\(a,b,c\)は三角形を形成する各辺を指している。
余弦定理の証明の前準備
以下の頂点ABC、各辺の長さabcの三角形があるとする。
そして、頂点Cから垂直に底辺と交差する点をHとする。
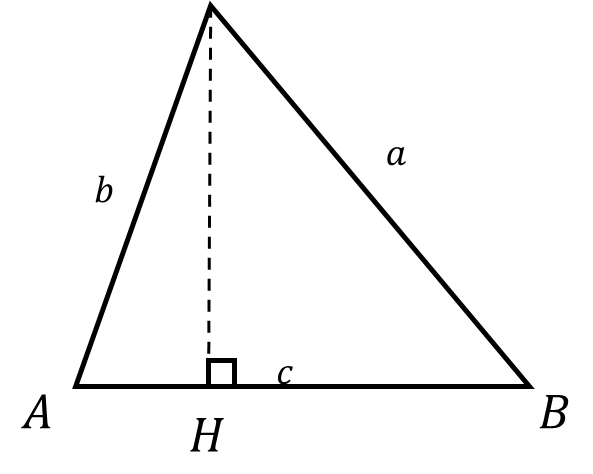
そして、abcでは以外の線の長さを求めると以下になる。
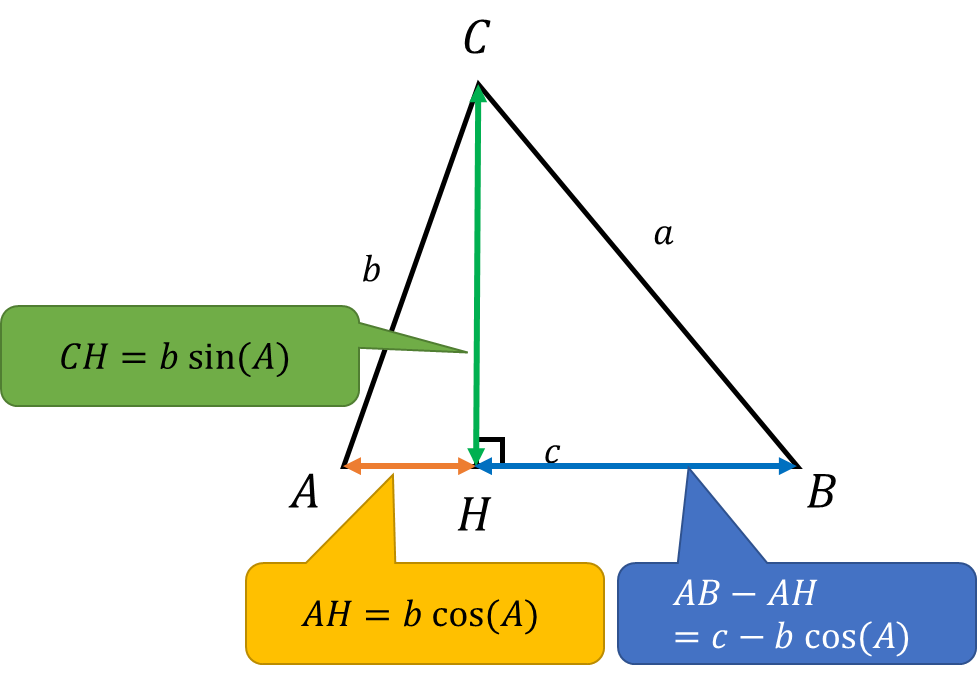
\(CH=b \sin(A)\)
\(AH=b \cos(A)\)
\(AB-AH=c – b \sin(A)\)
CHが垂直線のため、三角関数を用いて各線を求めることが可能。
加えて、三角比の基本公式として以下が必要となる。
\(\cos^2(\theta)+\sin^2(\theta)=1\)
公式は三平方の定理から求められる。
半径1の円起動の点と原点をを元に作った直角三角形を考えると以下の図になる。
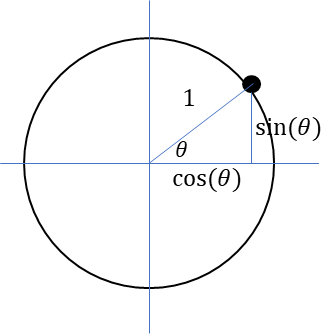
円軌道の点を元にしているので、半径が1。
よって、
底辺は\(\cos(\theta)\)
高さは\(\sin(\theta)\)
となる。
これを三平方に定理に当てはめれば、さっきの基本方式になる。
余弦定理の証明
三平方の定理より
\(a^2=|\vec{BC}|^2=|\vec{CH}|^2+|\vec{BH}|^2\)
\(=(b \sin(A))^2+(c-b\cos(A))^2\)
\(=c^2-2bc\cos(A)+b^2\cos^2(A)+b^2\sin^2(A)\)
三角比の基本公式
\(\cos^2(\theta)+\sin^2(\theta)=1\)
を使用し、
\(c^2-2bc\cos(A)+b^2\cos^2(A)+b^2\sin^2(A)\)
\(=c^2-2bc\cos(A)+b^2(\cos^2(A)+\sin^2(A))\)
\(=c^2bc\cos(A)+b^2\)
よって、
\(a^2=b^2+c^2-2bc\cos(A)\)
内積の定義と余弦定理から成分表記の内積を求める
なす角\(\theta\)となる\(\vec{a}\)と\(\vec{b}\)を元に以下の図を考える。
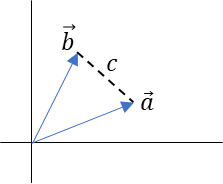
この場合、3辺の長さは以下となる。
\(a=|\vec{a}|\)
\(b=|\vec{b}|\)
\(c=|\vec{b}-\vec{a}|\)
ここに余弦定理を適用すると以下になる。
\(|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos(\theta)=|\vec{b}-\vec{a}|\)
上記を変形して、内積の定義と合わせると、
\(|\vec{a}||\vec{b}|\cos(\theta)=\displaystyle\frac{1}{2}(|\vec{a}|^2+|\vec{b}|^2-|\vec{b}-\vec{a}|)\)
そして、右辺を計算していくが、
\(\vec{a}\)の成分は\((a_1,a_2)\)
\(\vec{b}\)の成分は\((b_1,b_2)\)
とする。
\(\displaystyle\frac{1}{2}(|\vec{a}|^2+|\vec{b}|^2-|\vec{b}-\vec{a}|)\)
\(=\displaystyle\frac{1}{2}(a_1^2+a_2^2+b_1^2+b_2^2-(a_1-b_1)^2+(a_2-b_2)^2)\)
\(=\displaystyle\frac{1}{2}(2a_1 b_1+2a_2 b_2)\)
\(=a_1 b_1+a_2 b_2\)
つまり、以下が成立する。
\(|\vec{a}||\vec{b}|\cos(\theta)=a_1 b_1+a_2 b_2\)
これが成分表記による内積の公式となり、方程式と強い関係性を証明するものとなる。





コメント