【再掲】入力、出力パターン
まず、今回の単純パーセプトロンに対しての入力、出力のパターンを再掲しておこう。
| \(x_1\) | \(x_2\) | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
ANDゲートの真理値表になる。
入力パターンが増えると・・・。
入力パターンが増えると、連鎖律の考え方も少し変わる。
ひとつづつ学習するオンライン学習の場合は加味不要だが、
バッチ学習、ミニバッチ学習のように、ある程度の入力と出力(ラベル)のデータセットを一括で実施する場合、
連鎖律のルートが増えることになる。
図で書くとこんな感じになる。
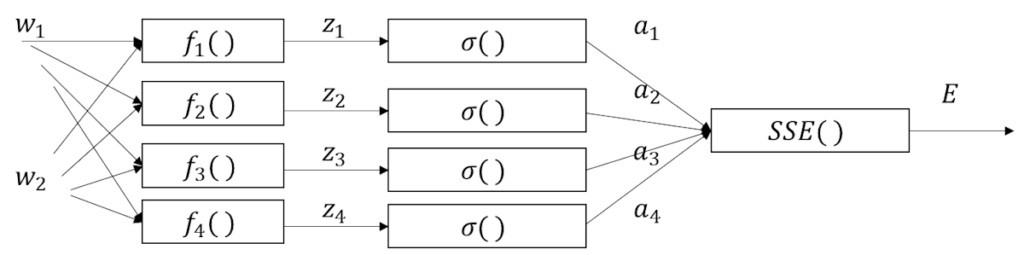
そして、数式で書くとこんな感じ。
\(
\displaystyle\frac{\partial E}{\partial w_1}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_1}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_1}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_1}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_1}
\)
\(
\displaystyle\frac{\partial E}{\partial w_2}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_2}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_2}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_2}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_2}
\)
ちなみにバイアスも似たような感じ。
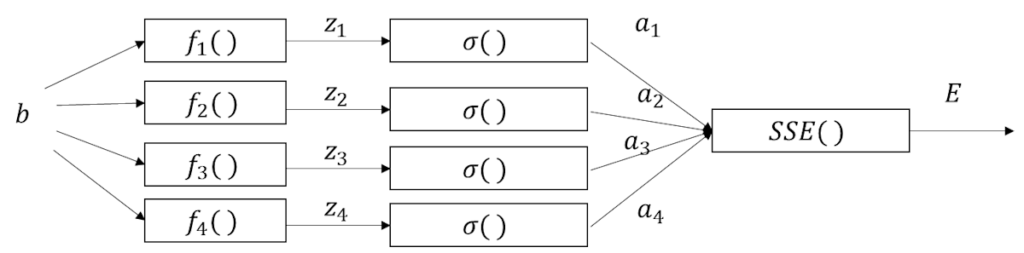
\(
\displaystyle\frac{\partial E}{\partial b}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial b}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial b}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial b}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial b}
\)
入力、出力が複数であるが故の連鎖律の事情のもう一つの考え方
以前、誤差関数の偏導関数を以下と示した。
\(
\displaystyle\frac{\partial E}{\partial A}=A-Y
\)
しかし、これは学習が一つのデータしか入れない場合の式。
誤差関数は二乗和誤差関数なので、
本来であれば、総和であるΣが付く。
よって、偏導関数も本来であれば以下になる。
\(
\displaystyle\frac{\partial E}{\partial A}=\sum_{i=0}^n(a_i-y_i)
\)
これを連鎖律に組み込む
\(
\displaystyle\frac{\partial E}{\partial A}=\sum_{i=0}^n(a_i-y_i)\cdot\sigma(Z)\{1-\sigma(Z)\}\cdot X
\)
Σで各連鎖律の総和を出すってことは前回の各ルートの連鎖律の合計を算出するのと同じことになる。
一応数式を書き出す、結果的に先ほどと同じものになる。
\(
\displaystyle\frac{\partial E}{\partial w_1}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_1}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_1}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_1}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_1}
\)
\(
\displaystyle\frac{\partial E}{\partial w_2}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_2}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_2}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_2}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_2}
\)
\(
\displaystyle\frac{\partial E}{\partial b}=
\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial b}
+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial b}
+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial b}
+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial b}
\)
一つ目がのがブロック図ベースの感覚的な捉え方で、
二つ目が数式ベースの理屈的な捉え方って感じになる。
どっちのアプローチが正しいかは良くわからないが、
結果的には同じものとなる。
次のページへ
次のページではプログラム化についての話となる。



コメント