【入門】逆伝播②【数値計算】

入力層の位置づけ
入力層の関数
入力層の偏導関数
バイアスの位置づけ
バイアスの偏導関数
まとめ

入力層の位置づけ

フクさん：
ブロック図と連鎖律に於ける入力層の位置づけを確認

ブロック図上での入力層の位置づけ

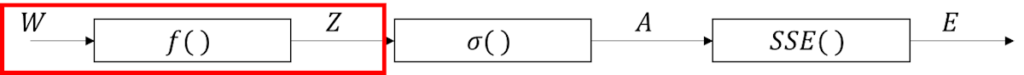
連鎖律上での入力層の位置づけ

\(
\displaystyle\frac{\partial E}{\partial W}=\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}{\color{red}\frac{\partial Z}{\partial W}}
\)

名前のまんまで入力の部分。
連鎖律では一番後ろになる。

入力層の関数

入力層の関数として示すと以下になる。

\(
f(W)=WX+b
\)

入力に重みを掛けてバイアスを加えてるだけとなる。

入力層の偏導関数

そして、入力層の偏導関数を求める。

\(
\begin{eqnarray}
\displaystyle\frac{\partial Z}{\partial W}&=&\frac{\partial f(W)}{\partial W}=\frac{\partial(WX)}{\partial W}\\
&=&\frac{\partial WX}{\partial W}+\frac{\partial b}{\partial W}=\frac{\partial WX}{\partial W}&=&X
\end{eqnarray}
\)

と言う感じでシンプルになる。
元の関数がベクトルとは言え、形状的には1次関数。
よって、偏微分するとシンブルになる。

バイアスの位置づけ

先ほど、入力層の偏導関数を求めたが、
同じタイミングでバイアスも逆伝播で求めることになる。
よって、バイアスについて同じように偏導関数を求める必要がある。

と言っても、やってみると分かるが、無視できるレベルのシンプルさになる。
(重みもシンプルだったけど、さらにシンプル)

そして、恒例の位置づけと数式を記載しておく。

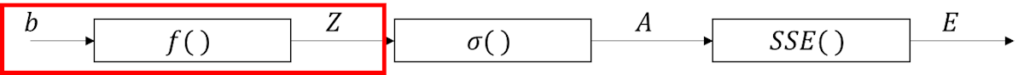
連鎖律上でのバイアスの位置づけ

\(
\displaystyle\frac{\partial E}{\partial b}=\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}{\color{red}\frac{\partial Z}{\partial b}}
\)

先ほどの重み\(W\)がバイアス\(b\)になっただけとなる。

バイアスの偏導関数

そして、先ほどの関数を元に偏導関数を求める。

\(
\begin{eqnarray}
\displaystyle\frac{\partial Z}{\partial b}&=&\frac{\partial f(b)}{\partial b}=\frac{\partial(WX+b)}{\partial b}\\
&=&\frac{\partial WX}{\partial b}+\frac{\partial b}{\partial b}=\frac{\partial b}{\partial b}&=&1
\end{eqnarray}
\)

なんと1になる。
\(b\)に着目すると、1次だし、係数も居ないから微分すると1になる。
と言っても、あくまで連鎖律の一部が1になるだけなので、
逆伝播全体で見れば誤差関数、活性化関数の影響は受ける。