MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第4章 その53【逆伝播④】
MATLAB,Python,Scilab,Julia比較 第4章 その54【逆伝播⑤】
MATLAB,Python,Scilab,Julia比較 第4章 その55【逆伝播⑥】
MATLAB,Python,Scilab,Julia比較 第4章 その56【逆伝播⑦】
を書き直したもの。
単純パーセプトロンに対する逆伝播についての話。
- 誤差関数の微分について。
- 活性化関数の微分について。
- 入力層の微分について。
- バイアスの微分について。
【再掲】逆伝播を想定した単純パーセプトロンの構成
まずは、逆伝播を想定した単純パーセプトロンの構成を再掲。

今回は、
誤差関数、活性化関数、入力層、バイアスの各ブロックの微分の話になる。
誤差関数の位置づけ
逆伝播を行う上で、連鎖律を解くわけだが、
基本的にはブロック図上の後ろから解いていく。
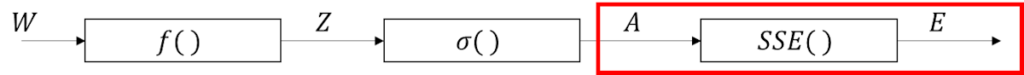
ブロック図的には後ろからということになるが、
連鎖律で見ると前からになる。
\(
\displaystyle\frac{\partial E}{\partial W}={\color{red}\frac{\partial E}{\partial A}}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial W}
\)
逆伝播として考えることからも、
誤差関数から考えるのが一般的ということになる。
誤差関数
誤差関数は二乗和誤差を1/2にした、ちょい変形したものを使用する。
これは以前説明したように、微分した際にシンプルな式になるため。
\(
\displaystyle E={\color{red}\frac{1}{2}}\sum_{i=1}^n(\hat{y}_i-y_i)^2
\)
誤差関数の偏導関数
これにAとYを代入したものが以下
\(
\displaystyle E=\frac{1}{2}\sum_{i=1}^n(A-Y)^2=\frac{1}{2}\sum_{i=1}^n(A^2-2AY+Y^2)
\)
これの偏導関数が以下になる。
\(
\displaystyle \frac{\partial E}{\partial A}=\frac{1}{2}\sum_{i=1}^n(2A-2Y)=\frac{1}{2}\sum_{i=1}^n(A-Y)
\)
イヤーな感じの数式見えたと思うが、
やってみたらそれほど複雑ではない。
活性化関数の位置づけ
ブロック図と連鎖律に於ける活性化関数の位置づけを確認
ブロック図上での活性化関数の位置づけ

連鎖律上での活性化関数の位置づけ
\(
\displaystyle\frac{\partial E}{\partial W}=\frac{\partial E}{\partial A}{\color{red}\frac{\partial A}{\partial Z}}\frac{\partial Z}{\partial W}
\)
ちょうど真ん中になる。
活性化関数の導関数
今回の活性化はシグモイド関数。
つまり、シグモイド関数の導関数が活性化関数の導関数ってことになる。
シグモイド関数の導関数については、以前のここでやった。
わすれているなら復習しておくと良いだろう。
シグモイド関数の偏導関数
シグモイド関数の導関数が分かっているから、偏導関数もほぼ確定するのだが、
一応書き出しておこう。
以下の式になる。
\(
\displaystyle\frac{\partial A}{\partial Z}=\sigma^\prime(Z)=\sigma(Z){1-\sigma(Z)}
\)
シグモイド関数を微分したものは、シグモイド関数で表現できてしまう。
活性化関数の必要な特性として、「微分ができること」というのがあるが、
それは逆伝播を実施するための偏導関数が定義できるかってことになる。
他の活性化関数も基本は微分可能。
中には確率分布関数みたいなものを使って、微分が困難なものもあるが、
その場合は、変分と言う微分の親戚みたいな手法で逆伝播可能な状態にしている。
変分は今回は扱わないので、そういうものがあるって程度で頭の片隅に置いておけばOK。
次のページへ
入力層、バイアスの微分の話。






コメント