一連の合成関数
先ほどの構成をブロック図として書き出したのが以下になる。
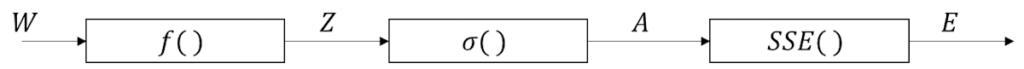
注意点としては、
入力が\(X\)ではなく重み\(W\)。
これは、調整したいのが入力ではなく重みであるため。
だから、単純パーセプトロンの学習における入力は重みと見なしてる感じになる。
そして、さきほどの合成関数を数式で表現するとこうなる。
合成関数
\(E=SSE(\sigma(f(W)))\)
各関数
そして、各関数を書き出す。
誤差関数
\(
\displaystyle E=\frac{1}{2}\sum_{i=1}^n(A-Y)^2
\)
活性化関数
\(
A=\sigma(X)
\)
入力と重みの内積
\(
Z=f(W)=
\begin{bmatrix}
w_1&w_2&b
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
1
\end{bmatrix}
\)
この関数の合成がさっきの合成関数ってことになる。
あとは、合成関数の微分こと連鎖律を考えていくことになる。
合成関数の微分こと連鎖律について
先ほどの関数の合成関数を元に連鎖律を定義できる。
以下の数式になる。
\(
\displaystyle \frac{\partial E}{\partial W}=\frac{\partial E}{\partial A}\frac{\partial A}{\partial Z}\frac{\partial Z}{\partial W}
\)
学習データを加味すると
そして、詳細は後ほど説明するが、
学習データを加味すると、\(f(W)\)は暗黙的に4種類になる、
結果的には以下の「多変量関数の連鎖律」になる。
\(
\displaystyle \frac{\partial E}{\partial w_1}=\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_1}+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_1}+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_1}+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_1}
\)
\(
\displaystyle \frac{\partial E}{\partial w_2}=\frac{\partial E}{\partial a_1}\frac{\partial a_1}{\partial z_1}\frac{\partial z_1}{\partial w_2}+\frac{\partial E}{\partial a_2}\frac{\partial a_2}{\partial z_2}\frac{\partial z_2}{\partial w_2}+\frac{\partial E}{\partial a_3}\frac{\partial a_3}{\partial z_3}\frac{\partial z_3}{\partial w_2}+\frac{\partial E}{\partial a_4}\frac{\partial a_4}{\partial z_4}\frac{\partial z_4}{\partial w_2}
\)
一見するとすごいことになっているように見える。
まとめ
- 誤差逆伝播法とか単純パーセプトロンに関連する用語を確認。
- 逆伝播を行う単純パーセプトロンの構成を確認。
- 一連の合成関数について書き出し。
- 合成関数を構成する各数式を書き出し。
- 合成関数の微分こと連鎖律について説明。
- 学習データを加味した場合の多変量関数の連鎖律について簡単に説明。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析



コメント