バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia4-backnumber/
はじめに
いままでは単純パーセプトロンによる線形分類だった。
今回から、非線形分類に突入。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
線形分類から非線形分類

これで、分類はばっちりだね。

いんや。
単純パーセプトロンでも分類できないものがある。

分類できないもの?
決定境界直線が引けるからだいたい行けそうな気がするけど?

そう。その決定境界直線が問題。
単純パーセプトロンは線形分類しかできない。

その言い方だと、非線形分類というものがありそうだな・・・。

正解。
非線形分類というカテゴリがあり、
それに対しては単純パーセプトロンでは実現不可能だ。

そうすると、単純パーセプトロン以外で実現ってことになるのか・・・。

まずは、非線形分類がどのようなものなのかを確認していこう。
非線形分類

いままで実施していた分類は線を一本引いて、決定境界を見つけ出す、
線形分類と呼ばれるもの。
しかし、世の中、線形分類だけでは分類できないものが多い。
例えば、論理ゲートのXORなどが代表的。
図で書くと以下だな。
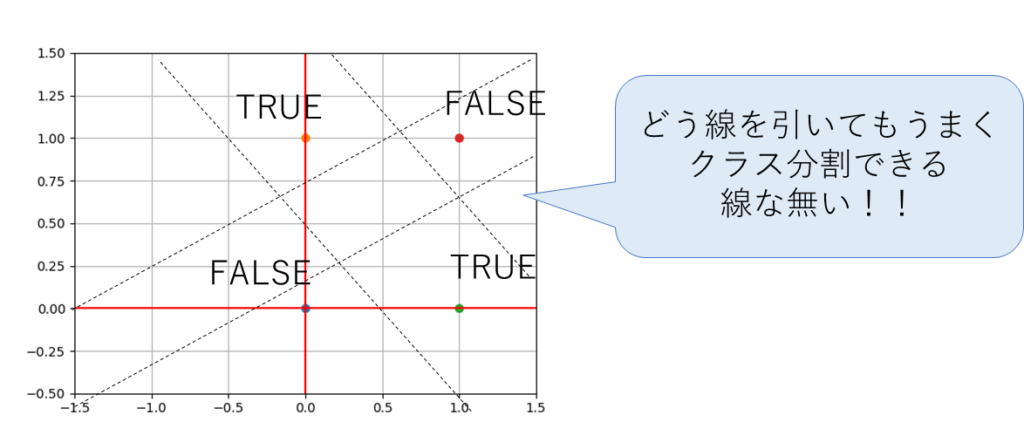

TRUEとFALSEが対角線上にいるから1本の線では上手くわけられないのか!

そうそう。
こういうものを「線形分離不可」「非線形分離」と言ったりする。
決定領域

で、どういうふうに分類されれば正解って言えるんだろう?

図にするとこんな感じだな。
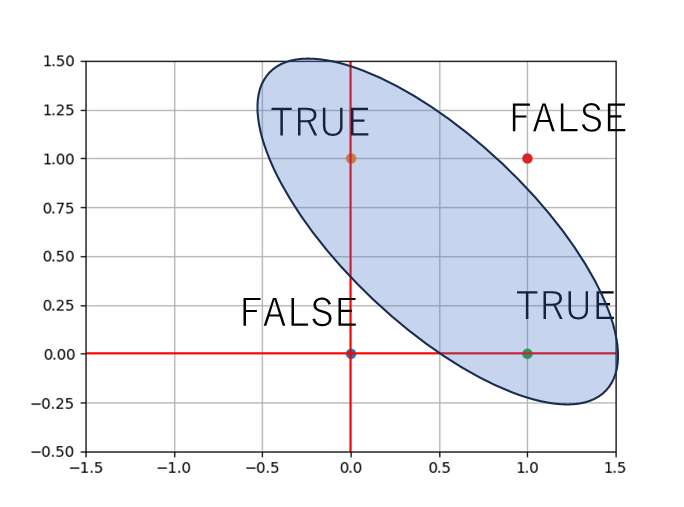

ほう。
楕円で囲えばいいのか。

この楕円部分を決定領域と言ったりする。
実際の分類の結果がこのようにキレイな楕円になるとは限らないけどね。
あくまで理想的な分類結果としてはこうなる感じってところだ。

で、何を使えばこれができそうなの?

それは次回説明!
まとめ

まとめだよ。
- 単純パーセプトロンでは分類できないものがある。
- XORなどの非線形分類を求められるものなどが代表的。
- 決定境界直線を求めるというより決定領域を特定するというイメージになる。
バックナンバーはこちら。
Pythonで動かして学ぶ!あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析




コメント