【入門】アフィン変換と畳み込みニューラルネットワーク【数値計算】

ニューロンが複数の場合
アフィン変換との関係性
まとめ

ニューロンが複数の場合

ニューロンを複数にした場合、
以下の図で表現できる。
尚、入力側の\(x\)の要素数、出力側の\(y\)の要素数は異なっていてOK。

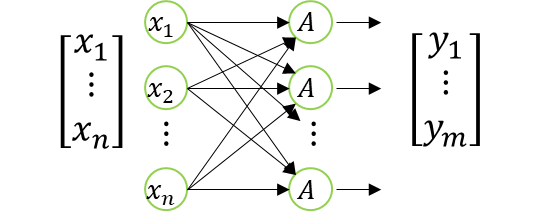
これも良く見かける画像だろう。
そしてこれを数式で表現する。

\(
\begin{bmatrix}
y_1 \\
\vdots \\
y_m \\
1
\end{bmatrix}=
A\Bigg(
\begin{bmatrix}
a_{11} & \dots & a_{1n} & b_1 \\
\vdots & \ddots & \vdots & \vdots \\
a_{m1} & \dots & a_{mn} & b_m \\
0 & \dots & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x_1 \\
\vdots \\
x_n \\
1
\end{bmatrix}
\Bigg)
\)

やべぇ感じになってきてはいるが、
数式で表現できるってことはわかるだろう。

アフィン変換との関係性

ここでアフィン変換の同次座標系の式を持ってくる。

\(
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}=
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\)

次元数は全然違うが、雰囲気的に全結合層と似ているのに気が付くだろう。
これが全結合層とアフィン変換の関係性になる。

といっても全結合層はアフィン変換をしているわけでは無い。
条件によってはアフィン変換のような座標変換として学習する層があってもおかしくはないが、
機能として別モノと思っておいた方が良い。

結局同じなのか別物なのかがわからんと思うが、
行列による一括変換という意味では同じ。
それに、全結合層は別名でアフィン層と言ったりする。
このアフィン層の由来は恐らくは、アフィン変換の同次座標系との類似から来ていると思われる。
このため、畳み込みニューラルネットワークとの兼ね合いを説明した。

あくまで余談であり、知らなくても問題の無い知識ではあるが、せっかくなので説明しておいた。