MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第3章 その65【アフィン変換⑨】
MATLAB,Python,Scilab,Julia比較 第3章 その66【アフィン変換⑩】
を書き直したもの。
アフィン変換の続き。
だが、ちょっと余談にそれる
畳み込みニューラルネットワークとアフィン変換の関係性について。
余談
キャンバス拡張も出来たところでアフィン変換に突入したいところだが、
その前に少し余談を入れておく。
以前やった畳み込み演算と今回のアフィン変換は
畳み込みニューラルネットワークと関連してる。
畳み込み演算は、名称的に関係ありそうなのはわかると思う。
アフィン変換側の関連性がイメージ沸きにくいだろう。
当然、アフィン変換自体がそのまま関係しているわけじゃないが、
無関係というわけでもない。
その点を少し知っておこうって程度の話になる。
畳み込みニューラルネットワークの構造
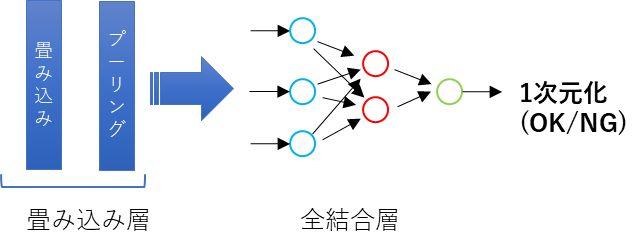
まず、畳み込みニューラルネットワークの基本的な構造を示す。
当然、さまざまネットワークがあるから、今回の説明に於いての前提としてこう解釈する
って意味合いになる。
興味ある人、畳み込みニューラルネットワーク、CNNでググってみると良いだろう。
畳み込み層
左側の畳み込み層。
厳密には畳み込み層とプーリング層がふくまれるわけだが、
これがやっているのはおおよそ以下。
- 輪郭検出
- 次元削減
- 抽象化
画像で示すとこんな感じになる。

畳み込み演算がベースになっているのがわかるだろう。
ニューロン
次に全結合層だが、その前にニューロンについて確認する。
ニューロンは以下で表現される。
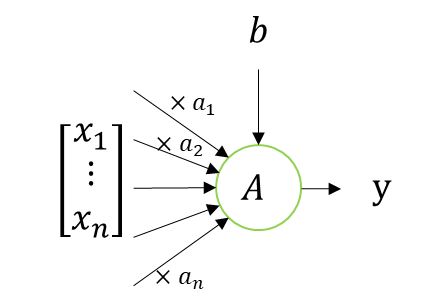
これも良く見る画像だと思う。
このニューロンの演算って実は、\(x\)ベクトルと重みの\(a\)ベクトルの内積と解釈できる。
数式を出すとこうなる。
\(
y=A\Bigg(
\begin{bmatrix}
a_1 & \dots & a_n & b
\end{bmatrix}
\begin{bmatrix}
x_1 \\
\vdots \\
x_n \\
1
\end{bmatrix}
\Bigg)
\)
計算としては一緒になる。
ニューロン一個だとこんな感じだが、
これが複数になるともう少しややこしくなる。




コメント