【入門】アフィン変換とアフィン行列【数値計算】

回転行列概要
動く点P
回転を直交座標系で捉える
回転行列
まとめ

回転行列概要

アフィン行列の回転の時に出た、回転行列について説明しておく。
まずはWikipediaから引用。

線型代数において、回転行列（かいてんぎょうれつ、英: rotation matrix）とは、ユークリッド空間内における原点中心の回転変換の表現行列のことである。
2次元や3次元の回転は、幾何学、物理学、コンピュータグラフィックスの分野での計算に非常によく使われている。大半の応用で扱うのはこのふたつの場合だが、一般の次元でも回転行列を定義することができる。
Wikiepdiaより(https://ja.wikipedia.org/wiki/%E5%9B%9E%E8%BB%A2%E8%A1%8C%E5%88%97)

ユークリッド空間とかが意味不明かもしれないが・・・。

ユークリッド空間は定義としてはいろいろあるのだが、
ここでは、我々が普通に認識できる2次元平面や3次元空間を指していると思って良いだろう。
(4次元以上のユークリッド空間も定義上は存在はする。)

動く点P

回転行列の具体的な話に突入するが、
ここでは2次元の回転行列について説明する。
3次元以上については割愛する。
(今回やるアフィン変換自体が2次元平面なので…。)

まず、とある平面上に点\(P\)が居るとする。
これを原点から見て回転角\(\theta\)分移動させる。
移動した先を点\(P\prime\)とする。
画像で示すと以下になる。

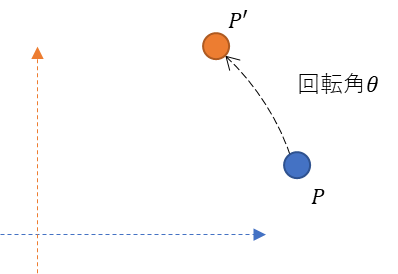
回転を直交座標系で捉える

で、問題は、この点\(P\)と点\(P\prime\)はどのくらい動いたか。
「回転角\(\theta\)分動いた」
のだが、これは極座標系の表現。
ここでは、直交座標系の表現が欲しい。

これを解決してくれるのが回転行列。

まず、回転角\(\theta\)の移動を直交座標系に直すには
\(\sin\)、\(\cos\)が使える。
画像で示すと以下になる。

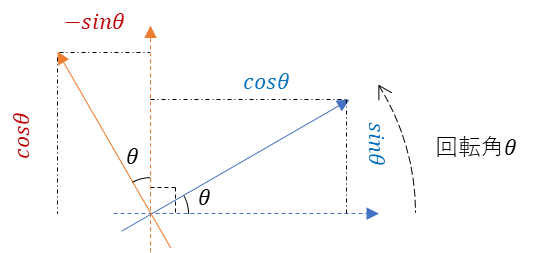
sin、cosによる極座標から直交座標へ、回転角θ、cosθ、sinθ、-sinθ、cosθ

原点を中心にx軸、y軸ごと移動したイメージになる。
基本ベクトルで表現すると分かるかもしれない。

関数\(\rm{R}\)が回転を示す関数とする。

x軸方向に1の基本ベクトルを回転角\(\theta\)分移動

\(
\rm{R}(\theta,
\begin{bmatrix}
1 \\
0
\end{bmatrix}
)=
\begin{bmatrix}
\cos\theta \\
\sin\theta
\end{bmatrix}
\)

y軸方向に1の基本ベクトルを回転角\(\theta\)分移動

\(
\rm{R}(\theta,
\begin{bmatrix}
0 \\
1
\end{bmatrix}
)=
\begin{bmatrix}
-\sin\theta \\
\cos\theta
\end{bmatrix}
\)

回転行列

そして、これらを合体させて行列にしたものが回転行列になる。
点\(P\)の座標を\(P_x,P_y\)
点\(P\prime\)の座標を\(P\prime_x,P\prime_y\)
とした場合、以下がその関係性になる。

\(
\begin{bmatrix}
P\prime_x \\
P\prime_y
\end{bmatrix}=
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
\begin{bmatrix}
P_x \\
P_y
\end{bmatrix}
\)

x軸とy軸を一括にやるから、
行列にまとめてしまえば良い。

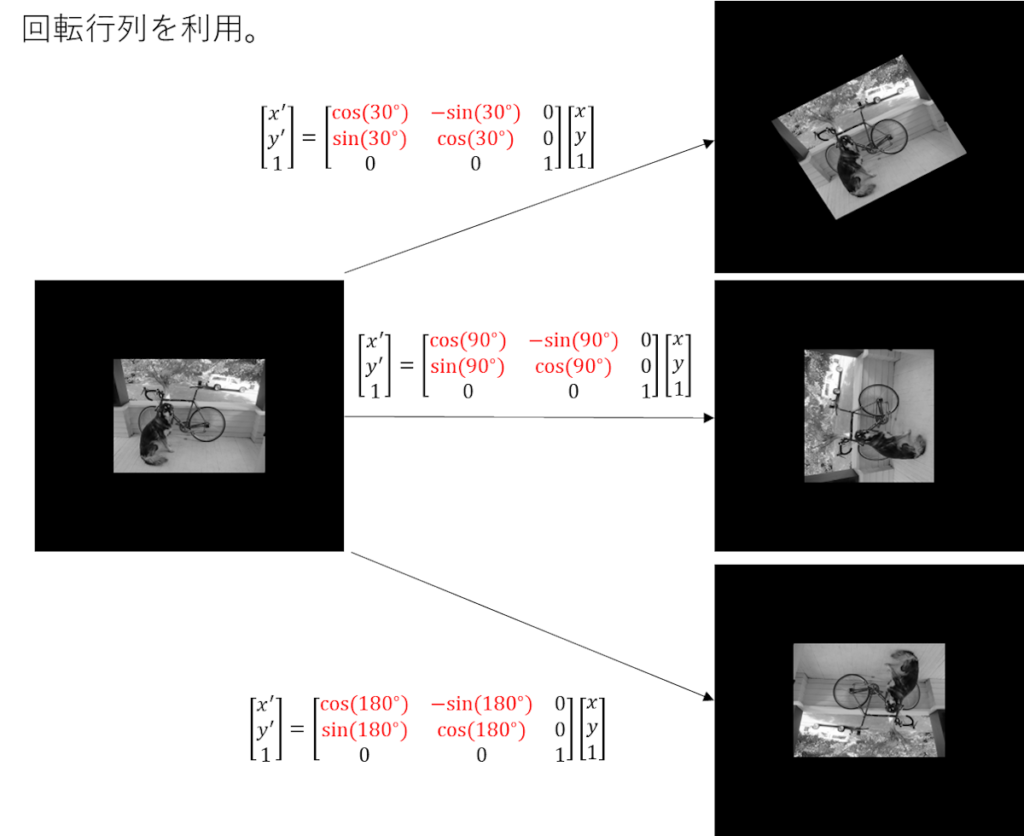
この座標の回転移動で使用される回転行列が
アフィン変換の回転時のアフィン行列に組み込まれてる。