MATLAB、Python、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第3章 その67【アフィン変換⑪】
MATLAB,Python,Scilab,Julia比較 第3章 その68【アフィン変換⑫】
を書き直したもの。
アフィン変換の続き。
以前言った、まだら模様問題の対策について。
まだら模様問題の対策としてシンプルな手法について。
まだら模様問題
以前言ったが、変換後にまだら模様になる問題が残っている。

これについて対策をする必要がある。
まだら模様が発生する原因
対策の前に原因。
原因が分からければ対策もできない。
原因は、
座標変換元より座標変換先の空間の方が広いため。
画像で説明すると以下になる。
縦横を2倍に伸長する場合を例としている。
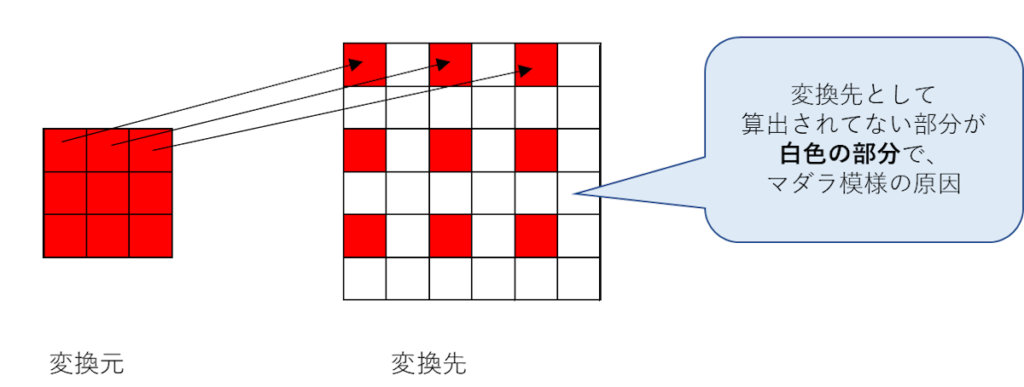
赤のところは変換元のピクセルからコピーされてるけど、白い部分へコピーするのがない。
これは、扱ってるデータが標本化されているから起きる事象。
アナログ的なものであれば、微小な座標変化を大きな座標変化にすればよい。
まだら模様問題の対策
原因がわかったところで対策の話になる。
一般的には以下の補間アルゴリズムを適用する。
- 最近傍補間(近傍のピクセルをコピー)
- バイリニア補間(線形補間の平面版)
- バイキュービック補間(周囲16点を3次式で同定して、その式を元に補間)
全体的結構めんどくさい。
よって、ここではもうちょいシンプルな手法を使うことにする。
まだら模様対策のシンプルなやつ
シンプルは手法を画像で示すとこんな感じになる。
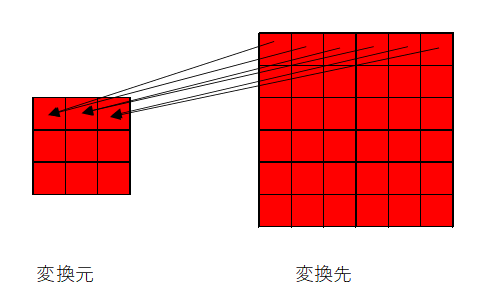
矢印の方向が、
変換元から変換先
じゃなくて、
変換先から変換元
になってる。
変換元から変換先にコピーするとピクセルが足りなくなるから、
だったら、変換先の全ピクセル位置から変換元を参照する方式にすれば、
ピクセルが足りないという事象は起きない。
これだったら全ピクセルが埋まるから、まだら模様が発生しない。
で、具体的にはどうするのか?
具体的にはどうすれば良いだろうか?
変換元から変換先にコピーするのがアフィン変換で、
それを逆向きにするのってできるのか?
いわゆるアフィン逆変換を用いることで可能になる。
アフィン逆変換
まず、アフィン変換の数式を再掲しよう。
\(
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}=
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}
\)
これを逆変換するということは、
以下のようなことをすればOK。
\(
\begin{eqnarray}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}&=&
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}\\
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}&=&
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}\\
\begin{bmatrix}
x\\
y\\
1
\end{bmatrix}&=&
\begin{bmatrix}
a & b & T_x\\
c & d & T_y\\
0 & 0 & 1
\end{bmatrix}^{-1}
\begin{bmatrix}
x\prime\\
y\prime\\
1
\end{bmatrix}\\
\end{eqnarray}
\)
つまり、逆行列を使えばOK。
まとめ
- アフィン変換後にまだら模様になる問題がある。
- まだら模様対策のシンプルなやつを確認。
- アフィン逆変換を使う。
- アフィン逆変換は、アフィン変換の式を変形しただけ。
- アフィン行列が逆行列になる。
MATLAB、Python、Scilab、Julia比較ページはこちら





コメント