MATLAB、Scilab、Scilab、Julia比較ページはこちら
https://www.simulationroom999.com/blog/comparison-of-matlab-python-scilab/
はじめに
の、
MATLAB,Python,Scilab,Julia比較 第2章 その23【最小二乗法㉒】
を書き直したもの。
平均、分散、共分散を用いた1次関数最小二乗法の係数算出について。
前回で数式としては導出できたが、
分散、共分散について一部説明しておく必要がある。
(不偏分散、不偏共分散)
不偏？標本？
本来であれば、MATLAB等で平均、分散、共分散を利用した1次関数最小二乗法を試すところだが、
実際にプログラムを組む際に
不偏分散、不偏共分散、標本分散、標本共分散の話にぶち当たる可能性が高い。
というわけで、先に不偏分散、不偏共分散、標本分散、標本共分散を説明しておく。
標本分散と不偏分散の数式比較
まず標本分散と不偏分散を数式で確認する。
標本分散
\(
\displaystyle\sigma^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2
\)
不偏分散
\(
\displaystyle s^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2
\)
前回までで出てきた、分散は標本分散の方となる。
不偏分散とは
ところで不偏分散は何者だろうか？
若干計算式は異なるが、標本分散と似たよう特性にはなりそう。
まず、統計としては、
全データを対象とした記述統計と
母集団から一部をサンプルして、母集団を推定する推測統計に分かれる。
推測統計側は全データがそろってないけど、母集団を推測するには十分なデータがそろってる前提はある。
そこで標本分散と不偏分散を見比べてると、
標本分散＜不偏分散
となることがわかると思う。
\(\displaystyle \frac{1}{n}\)と\(\displaystyle \frac{1}{n-1}\)の差でそうなる。
推測統計に於いて、標本分散を行うと実際の分散より小さくなる傾向がある。
証明方法は割愛するが、以下のイメージになる。
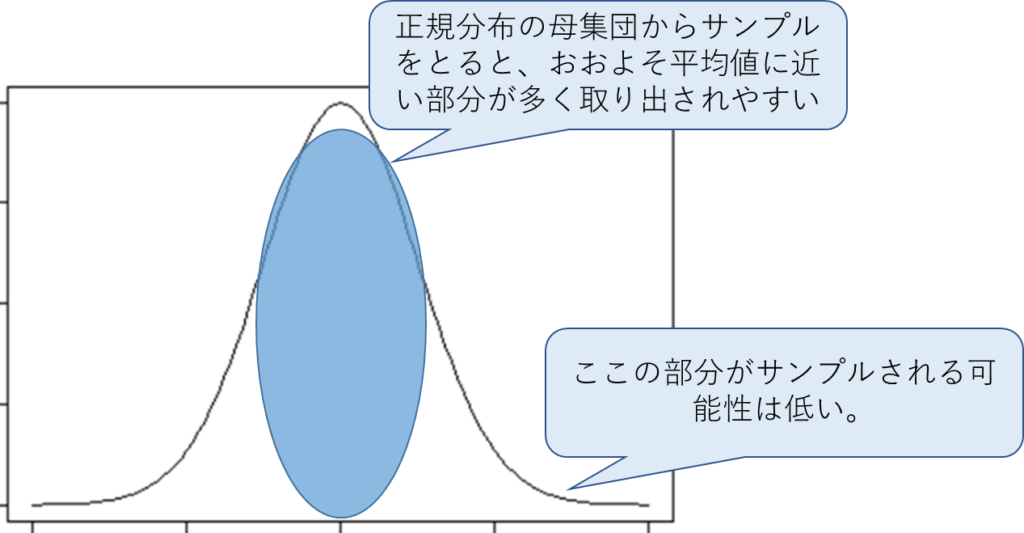
前提として母集団は正規分布に従うとしている。
ポイントは正規分布に対してサンプルをとると、平均値に近い部分からサンプルが取り出される可能性が高い点。
そうなると、分散はどうなるか？
恐らく、母集団の分散より、サンプルした方の分散の方が小さくなる。
そのため、不偏分散ではやや大きくして、母集団の分散に近づけている。
\(\displaystyle \frac{1}{n}\)と\(\displaystyle \frac{1}{n-1}\)の\(n\)が大きくなれば、
両者の差を減っていくので、サンプル数が多くなると、不偏分散でも母集団の分散に近付くのもわかるだろう。
なぜ不偏分散の話が出た？
最小二乗法で実際に使うのは標本分散であり、不偏分散ではない。
よって、不偏分散の情報は不要のように見える。
これは、各ツール、各言語の分散、共分散を算出してくれる関数の性質に理由がある。
各ツール、各言語で分散、共分散を計算してくれる関数があるのだが、
大体がデフォルトで不偏分散を算出してくる。
一応、オプションを追加することで、標本分散を取得できることが多い。
だけど、標本分散、不偏分散の存在とその意味を理解してないとたぶん迷子になる。
これを理由として、標本分散、不偏分散の存在を先に知ってもらったわけである。
共分散の方
理屈は一緒だが、
共分散も母集団全体か標本かで2パターンになる。
これも各ツール、各言語の関数で得られるがオプションでの切り替えが必要になる。
標本共分散
\(
\displaystyle \sigma_{xy}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})
\)
不偏共分散
\(
\displaystyle s_{xy}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})
\)
まとめ
- 標本分散と不偏分散について説明。
- 証明方法は割愛。
- 図を見て、不偏分散の必要性を察っするレベルで確認。
- 各ツール、各言語で分散を求める関数等があるが、大体が不偏分散。
- オプション指定で標本分散にすることも恐らく可能。
MATLAB、Python、Scilab、Julia比較ページはこちら
Pythonで動かして学ぶ！あたらしい線形代数の教科書
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロからはじめるPID制御
OpenCVによる画像処理入門
恋する統計学[回帰分析入門(多変量解析1)] 恋する統計学[記述統計入門]
Pythonによる制御工学入門
理工系のための数学入門 ―微分方程式・ラプラス変換・フーリエ解析
コメント