バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回は内積の定義から。
内積は単なる計算方法であり、内積そのものにに意味はない。
ただし、相関性、類似成分抽出、方程式の別表現などの特性はある。
そして、その方程式に繋げるために余弦定理とかが必要。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
余弦定理

内積と方程式を繋ぐためには
余弦定理というものが必要なので、これを知ってもらおう。

うーん、なんか聞いたことはあるようなないような・・・。

Wikipediaが割としっかり解説してるな。
とりあえず引用しよう。
余弦定理(よげんていり、英: law of cosines, cosine formula)とは、平面上の三角法において三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理である。余弦定理を証明するために用いられる補題はときに第一余弦定理と呼ばれ、このとき証明される定理は第二余弦定理と呼ばれ区別されることがある。単に余弦定理と言った場合、第二定理を指す。
Wikipediaより(https://ja.wikipedia.org/wiki/%E4%BD%99%E5%BC%A6%E5%AE%9A%E7%90%86)

そして、Wikipediaにある通り、今回言ってる余弦定理は第二余弦定理の方で、
第二余弦定理は以下になる。
\(a^2=b^2+c^2-2ab\cos(\alpha)\)

というか、ここで出てくる\(a,b,c\)はなんだ?

三角形を形成する各辺を指している物だな。

うーん、そもそも余弦定理でハマってしまった感じだ・・・。

まじか。
線形代数の基礎の前に余弦定理の証明の話をした方が良いかもしれんな。

説明出来そうならお願いしたいかな・・・。
余弦定理の証明の前準備

まず、以下の頂点ABC、各辺の長さabcの三角形があるとする。
そして、頂点Cから垂直に底辺と交差する点をHとする。
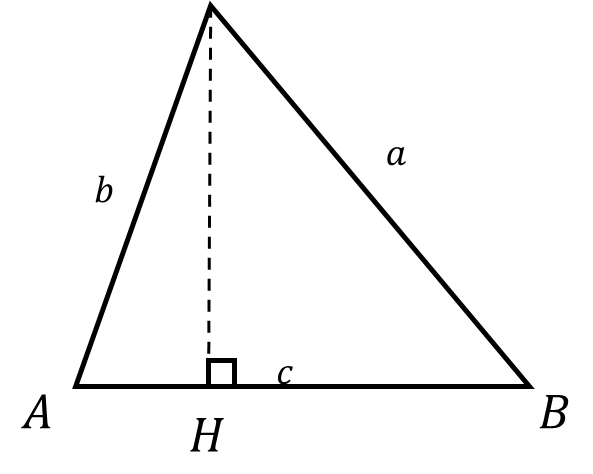

つまり、直角三角形とかじゃない一般的な三角形ってことだね。

そして、abcでは以外の線の長さを求めると以下になる。
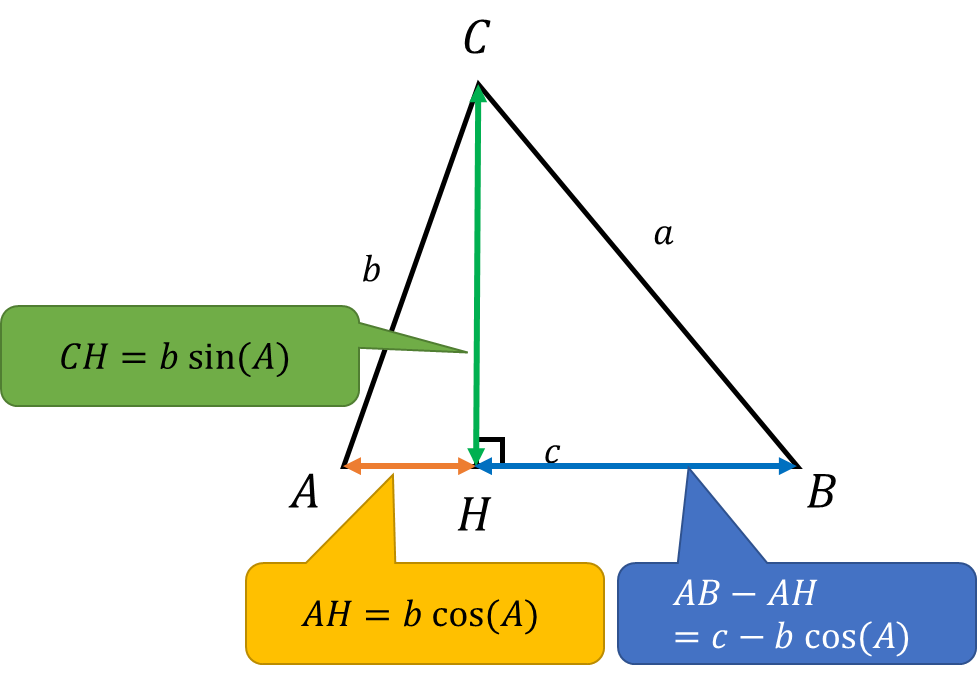
\(CH=b \sin(A)\)
\(AH=b \cos(A)\)
\(AB-AH=c – b \sin(A)\)

そうか、CHが垂直だから、三角関数を使って求められる線があるのか。
三角比の基本公式

あと、三角比の基本公式で以下がある。
\(\cos^2(\theta)+\sin^2(\theta)=1\)

足したら1になるの?

この公式は三平方の定理から求められる。
半径1の円起動の点と原点をを元に作った直角三角形を考えると以下の図になる。
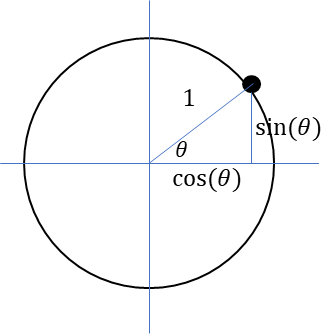

円軌道の点を元にしているので、半径が1なので、
底辺は\(\cos(\theta)\)
高さは\(\cos(\theta)\)
となる。

なるほど。
あとは、三平方に定理に当てはめれば、さっきの基本方式になるのか。

そうそう。
余弦定理の証明

ここから一気に証明になる。
三平方の定理より
\(a^2=|\vec{BC}|^2=|\vec{CH}|^2+|\vec{BH}|^2\)
\(=(b \sin(A))^2+(c-b\cos(A))^2\)
\(=c^2-2bc\cos(A)+b^2\cos^2(A)+b^2\sin^2(A)\)
三角比の基本公式
\(\cos^2(\theta)+\sin^2(\theta)=1\)
を使用し、
\(c^2-2bc\cos(A)+b^2\cos^2(A)+b^2\sin^2(A)\)
\(=c^2-2bc\cos(A)+b^2(\cos^2(A)+\sin^2(A))\)
\(=c^2bc\cos(A)+b^2\)
よって、
\(a^2=b^2+c^2-2bc\cos(A)\)

おー、余弦定理が求まったぞ!
まとめ

まとめだよ。
- 余弦定理を何とか証明。
- 垂直線を使って2つの直角三角形を作ることで各辺を三角関数を使用した表現が可能。
- 三角比の基本公式を加えると、余弦定理が求まる。
- 基本公式は三平方の定理と半径1の円起動の点と原点をを元に作った直角三角形から求まる。
バックナンバーはこちら。




コメント