バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
とりあえず、線形代数の基礎はやっておく方針となった。
流れとしては以下。
- 行列の内積の公式の再確認。
- 方程式と内積。
- 連立方程式と行列。
- 行列によるベクトル変換。
- 行列によるベクトル群変換。
今回は、「方程式と内積」から。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
内積の定義

まず、「方程式と内積」の関係性の話になるが、
その前に内積の定義を確認しておこう。

ぶっちゃけ内積って何やってるか意味わからんしね。
計算方法は分かるけど、この答えが何なのかってのが不明だ。

その気持ちはわかるが、
内積は、掛け算、割り算と同じく、そういう計算方法ってだけだな。
そこに意味はない。
「内積を問う」ということは「掛け算や割り算を問う」のと一緒だな。

まじかよ・・・意味不明だとは思ってたけど、そもそも意味が無かったなんて・・・。

ただ、特性のようなものはあるな。
まずは内積の定義を確認しよう。
\(
\vec A \cdot \vec B = |A||B|\cos(\theta)
\)

演算子は省略されることもあるが、
基本的には”\(\cdot\)”になる。
このことからドット積とも呼ばれるな。
そして、計算結果がベクトルからスカラーになることから
スカラー積とも呼ばれる。

別名が多いな・・・。

私が説明する場合は、「内積」に統一するとしよう。
内積の特性

そして、内積の特性だが、2つのベクトルの相関性を知ることができる。

相関性?

\(|a||b|\cos(\theta)\)を図示するとこうなる。
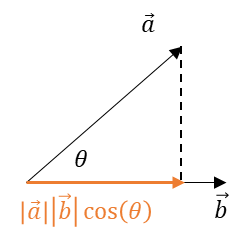

なるほど。
cos(θ)だから、こういう関係性になるのか。

そして、\(\vec b\)のノルム(大きさ)が1とした場合、
内積の結果が1に近いほど\(\vec a\)と\(\vec b\)は似ている。
ってことになる。

ほう!それは面白い関係性だ!

この考え方は類似度と呼ばれてて、
特に今回のやり方はcos類似度って呼ばれてるな。

他にもなんか便利な特性が有ったりするの?

いずれ説明するとは思うが、畳み込み積分(合成積)そのものであったり、
それを利用した類似成分の抽出だったり、
今回説明予定の方程式と強い関係性があったりで、
様々な数学的テクニックの基本となっている。
だから、最初に言ったように、内積を問うということは掛け算割り算を問うことと一緒だ。

なるほど。
途中何言ってるかさっぱりわからんかったけど、、
基本過ぎるから意味を持たないってことになるのかー。

(「言ってることがさっぱりわからん」ってところから、なぜなるほどになったのか・・・。)
まとめ

まとめだよ。
- 内積の定義を確認。
- 内積は単なる計算方法であり、内積そのものにに意味はない。
- ただし、特性のようなものはある。
- 内積の分かり易い特性としては相関性。
- 類似度とも言われ、特に内積を利用したものをcos類似度と呼ばれる。
- 基本的な計算であるが故に畳み込み積分、類似成分抽出、方程式などに利用される。
バックナンバーはこちら。



コメント