バックナンバーはこちら。
https://www.simulationroom999.com/blog/compare-matlabpythonscilabjulia-backnumber/
はじめに
前回は、逆行列を求める掃き出し法について説明。
対角以外を0にするようにし、最後に対角成分で行全体を割ればOKなので、
プログラム化しやすい部類ではある。
とわいけ結構めんどくさいろじっくではある。
しかし、MATLAB、Python(Numpy)、Scilab、Juliaでは逆行列を求める機能があるので、直に計算することはない。
よって、今後は特に掃き出し法を使って逆行列を求めるってことはしない想定。
今回は、連立方程式について?
登場人物
博識フクロウのフクさん
イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん
イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
そもそも連立方程式って何ぞ?

行列を利用すると連立方程式が簡単に解けるのはわかったんだが・・・。

まだ、何かあるの?

よくよく考えると連立方程式って何が求まってるんだ????

(マジで言ってるのか?まぁマジなんだろうな・・・。(デジャブ))
交点を求める。

連立方程式は、複数の関数の交点を求めている。

交点?

まず以下の2つの関数があるとして、
\(
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 7 \\
x – y = -1
\end{array}
\right.
\end{eqnarray}
\)

これを図を使って交点を求めるとこんな感じ。
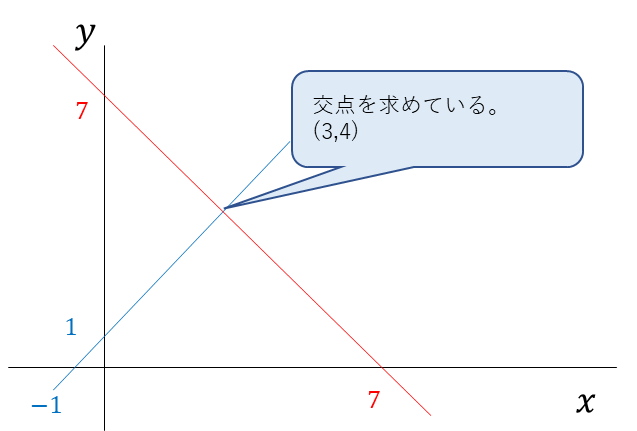
行列で求めると。

これを行列で求めると
\(
\begin{bmatrix}
x \\
y
\end{bmatrix}=
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}^{-1}
\begin{bmatrix}
7 \\
-1
\end{bmatrix}=
\begin{bmatrix}
3 \\
4
\end{bmatrix}
\)

ほう、交点が確かに求まった!
ためしにMATALBで計算

MATLABでこの行列計算させると
こんな感じになる。
>> inv([1 1;1 -1])*[7;-1]
ans =
3
4
一撃かー!
交点が求まると何がうれしいのか?

いやまてよ。
そもそもなぜ交点を求めるのか?

あんまり、行き過ぎると哲学の世界に突入しちゃうよ!

まぁ、若干過激な話になるが、
戦闘機にミサイルを命中さえるのは、交点を知っている必要はあるな。
自動運転とかも、自車以外の移動体の予測した上で交点を求めないと衝突回避とかもできないし。
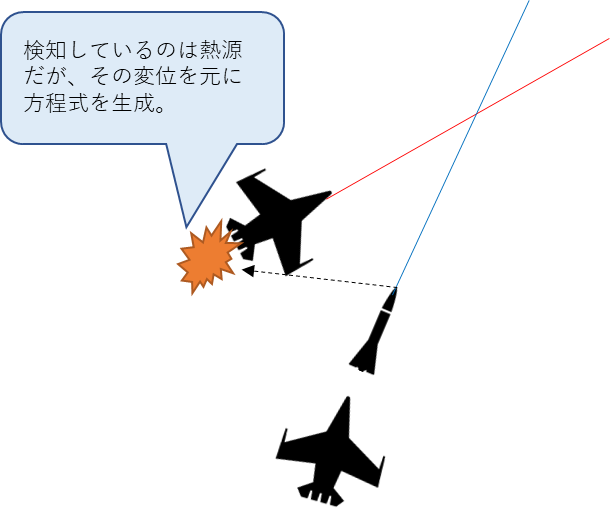

なるほど。
予測線を関数と見なすと確かに交点を求める局面は多そうだ。
まとめ

まとめだよ。
- 連立方程式を解くということは複数の関数の交点を求めるということ。
- 行列はそれを一撃で解ける。
- ためしにMATLABで算出したら一撃。
- 移動体の予測線を関数と見なすと、交点を求める重要性がわかりやすいかも?
バックナンバーはこちら。




コメント