バックナンバーはこちら。
https://www.simulationroom999.com/blog/stock-predict-matlabpython-backnumber/
はじめに
前回は、フーリエ変換、逆フーリエ変換のMATLABコードを作成してきた。
数式上でΣ、内積で表現できればプログラム化は容易ということもわかった。
今回は、実際にMATLABコードを動作させてみる。
登場人物
博識フクロウのフクさん

イラストACにて公開の「kino_k」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=iKciwKA9&area=1
エンジニア歴8年の太郎くん

イラストACにて公開の「しのみ」さんのイラストを使用しています。
https://www.ac-illust.com/main/profile.php?id=uCKphAW2&area=1
フーリエ変換、逆フーリエ変換(MATLAB版)

じゃ、前回のフーリエ変換、逆フーリエ変換のMATLAB版コードを動作させてみよう。
・・・実行中・・・

波形が取れた。
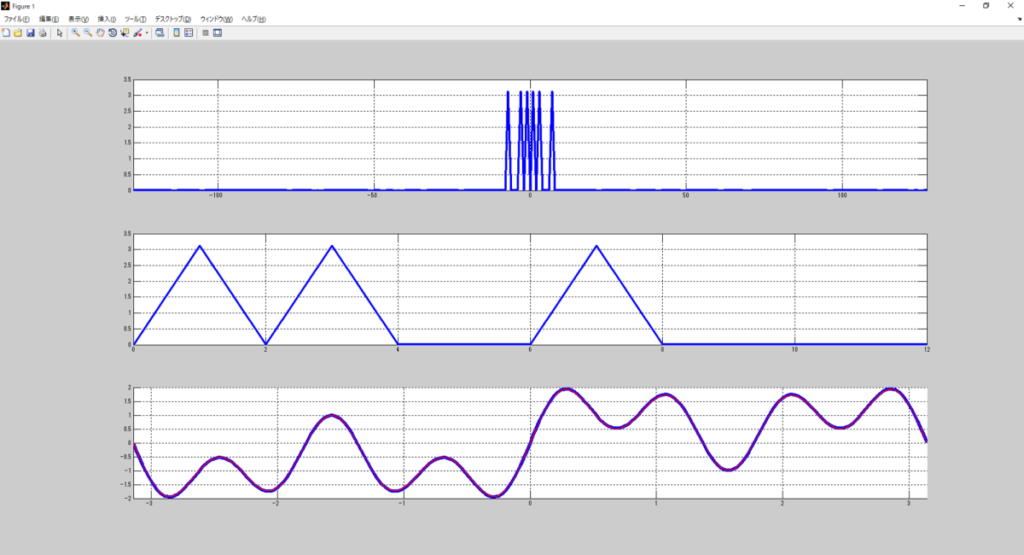

これはバッチリ動いてるじゃない?
1[Hz]、3[Hz]、7[Hz]が取れてるし。

うむ。
これがFFTと同等の周波数粒度で動作した場合の結果だな。

は?
FFTと同等?
あれ?

現在の\(\omega_{max}\)の設定値だとFFTと同等で、整数倍の周波数しか取れない。
周波数粒度を上げるには?

FFTと同等じゃダメじゃん!
FFTよりも細かく取るのが目的なのに!

周波数粒度を引き上げるには、\(\omega_{max}\)の設定値を弄れはOKだ。

現在は127[Hz]になっているんで、
20[Hz]くらいにしたらいいんじゃないかな?

じゃ、そこだけ20に書き換えて実行。
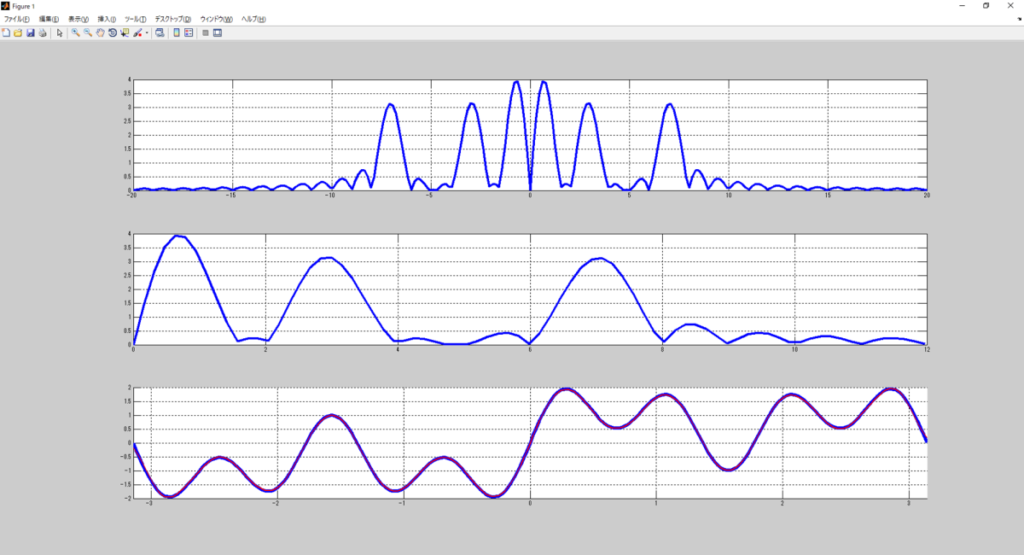

お!
これはかなり細かい周波数分布が取れてるじゃない?

どうやらうまく行ったようだな。
FFTじゃなくてもいいんじゃない?

こんなことが出来るならFFTじゃなくてフーリエ変換をそのままプログラム化した方がいいじゃん!
って思った。

それはどうかな?
周波数特性の粒度は細かくできるが、
処理速度はそれほど早くない。
今回はデータ数が少ないから、速度的な差は感じられないだけで。

そうか。
FFTは高速化アルゴリズムが入ってるって利点があるのか・・・。

と、すると、株価予測も時間掛かったりするの?

いや、大丈夫だ。
現状予測している範囲が1年分のデータなんで、
データ数としては250程度だ。
この程度であれば、今回のプログラムでも一瞬で終わる。

なんだ。
それは安心だ。

後は、メンドクサイけどPython(Numpy)で同じことをやってみるか。

(とうとう、素でメンドクサイ言い出したぞ)
まとめ

まとめだよ。
- フーリエ変換、逆フーリエ変換のMATLABコードを動作させてみた。
- まずはFFTと同等の整数倍の周波数特性。
- 最大周波数を調整すると細かい周波数特性が取れる。
- FFTよりも処理負荷が大きい演算になる。
- 今回扱う株価予測のデータ数程度であれば問題にはならない。
バックナンバーはこちら。




コメント